Soit a et b deux nombres donnés.

Lorsque l'on associe à chaque nombre la somme, on définit la fonction affine de coefficients

On lit "à tout  on associe le nombre " ou " a pour image a"

On lit " de égal "

On dit que  est l'image de  et que  est l’antécédent de

On calcule en fonction de, a et b sont des coefficients.

Exemple :

Soit

Quelle est l’image de 7 par la fonction f ?

L’image de 7 par la fonction  est 23.

Autre exemple :

Soit la fonction

Calculer l'antécédent de par la fonction g.

D’où l’équation :

L'antécédent de par la fonction est

Si  la fonction est de la forme , la fonction est appelée fonction linéaire.

Si  la fonction est de la forme , la fonction est appelée fonction constante.

Exemples

            est une fonction affine

                    est une fonction affine linéaire

                       est une fonction affine constante

Soit f la fonction affine définie par :

L'ensemble des points de coordonnées 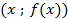 (noté 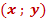) est appelé représentation graphique de la fonction affine.

Dans un repère, cette représentation est une droite.

Cette droite a pour équation :

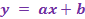
Elle est parallèle à la droite représentative de la fonction linéaire associée d’équation

"" est le coefficient directeur de la droite. Il indique " l'inclinaison " appelée la pente de la droite

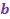«  » est l’ordonnée à l’origine.

Soit la fonction affine :  

Remarque :

Pour tracer une droite, représentant une fonction affine, il faut connaître deux de ces points que l’on choisira de façon à simplifier les calculs

Mode opératoire	Fonction f affine
Détermination des coordonnées de deux points de la droite Choix de deux abscisses Calcul des ordonnées correspondantes Conclusion : Présentation des coordonnées des points

En résumé

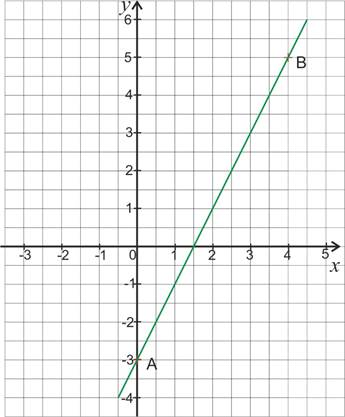
	A	B
x	0	4
y	–3	5

Construction de la droite

Soit les fonctions affines particulières :

Mode opératoire	Fonction g linéaire	Fonction h constante
Détermination des coordonnées de deux points de la droite Choix des abscisses Calcul des ordonnées correspondantes Conclusion : Présentation des coordonnées	Un seul point suffit autre que	Tous les points  conviennent Aucun calcul

En résumé :

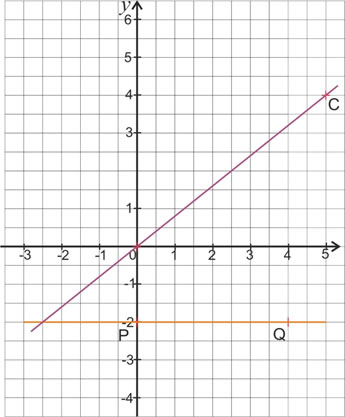
	O	C
x	0	5
y	0	4

	P	Q
x	0	4
y	–2	–2

Soit a et b deux nombres relatifs et f une fonction affine telle que

Pour deux nombres distincts x₁ et x₂ on a :

Ou encore :

Autrement dit, pour une fonction affine, les accroissements des valeurs de f (x) sont proportionnels aux accroissements des valeurs de x.

Et le coefficient de proportionnalité est le coefficient directeur (la pente) de la droite représentative.

Cette propriété permet de calculer le nombre a puis le nombre b connaissant les images de deux nombres.

Exemple :

Soit une fonction affine de type  à définir sachant que :

Présentation des données du problème

Soit une fonction affine de type





Or, si a et b sont deux nombres relatifs et f une fonction affine telle que , alors pour deux nombres distincts x₁ et x₂ on a :



Calcul de la valeur de a











Calcul de la valeur de b

On remplace «  » par sa valeur dans une des deux équations au choix.







Conclusion

La fonction affine  est :

Par une fonction linéaire, l'image d'une somme est la somme des images.

Si f est une fonction linéaire et x₁ et x₂ deux nombres alors :

Exemple :

Soit la fonction g telle que  et

Calculer l'image de

Par une fonction linéaire, l'image d'un produit par un nombre est le produit par ce nombre de l'image.

Si f est une fonction linéaire, x un nombre et k un nombre donné, alors :

Exemple :

Soit la fonction g telle que g(2,5)  =  10 et le nombre k  =  5

Calculer l'image de g(12,5)

Remarque :

Cette propriété peut s’écrire :