- Définitions
- Côté adjacent
- Cosinus d'un angle
- Utilité
- Conditions à satisfaire
- Définition
- Constatation
- Propriété
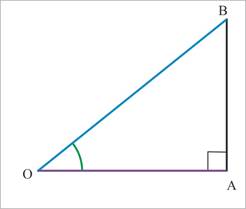
Le côté adjacent à un angle aigu dans un triangle rectangle est le côté qui forme cet angle avec l’hypoténuse.
Dans le triangle OAB rectangle en A [OB] est l’hypoténuse [OA]
est le côté adjacent à l’angle |
|
|
|
||||||||||||||||||
|
|
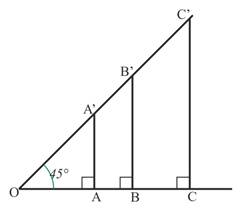
Pour un même angle aigu dans un triangle rectangle il y a proportionnalité entre le côté adjacent à cet angle aigu et l'hypoténuse.
Remarques :
Le coefficient de proportionnalité dépend de la valeur de l'angle
L’application du théorème de Thalès à cette configuration permet de démontrer cette propriété. En effet, (AA’), (BB’), (CC’)… sont parallèles donc :
- Définition
- Notation et exemple
- Utilisation de la calculatrice
Dans un triangle rectangle, le cosinus d’un angle aigu est égal au quotient du côté adjacent à cet angle par l’hypoténuse.
Remarque
Le cosinus est le coefficient de proportionnalité entre le côté adjacent et l’hypoténuse
Dans le triangle ABC rectangle en A : L’hypoténuse est le côté [BC]. Le
côté adjacent à l’angle Le
côté adjacent à l’angle Le cosinus de l’angle
Le cosinus de l’angle
|
|
- Pour obtenir la valeur du cosinus d’un angle, il faut
taper la touche
puis la valeur de l’angle. - Pour obtenir la valeur d’un angle à partir de son cosinus,
il faut taper
puis la valeur du cosinus ou du calcul qui permet de le calculer
Attention : Vérifier que la calculatrice est bien réglée en degré
Exemple :
Le cosinus de 50 ° : |
 |
Résultat : 
Remarque :
Le plus souvent, on obtient des valeurs approchées
Exemple :
L’angle dont le cosinus est 0,75 : |
 |
Résultat : 
Le cosinus d’un angle aigu dans un triangle rectangle, sert à calculer une longueur (quand on connait un angle) ou à calculer un angle aigu (quand on connait des longueurs).
- Pour calculer une longueur
- un triangle rectangle
- la longueur d’un côté et la mesure de l’angle aigu formé par ces deux côtés.
- Pour calculer la mesure d’un angle aigu :
- un triangle rectangle
- les longueurs des deux côtes formant cet angle.
Il faut :
Il faut :
- Applications
- Calcul de la longueur d'un segment
- Calcul de la mesure d'un angle
Pour calculer la longueur d’un côté de l’angle droit dans un triangle rectangle, il est nécessaire de connaître la mesure d’un angle aigu et la longueur de l’hypoténuse.
- Exemple 1
- Exemple 2
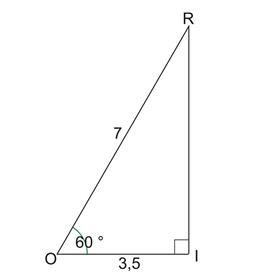
Le triangle
ROI est rectangle en I, 
Calculer la longueur du segment [IO].
On sait que, ROI est un triangle
rectangle en I tel que Or, dans un triangle rectangle le cosinus d’un angle aigu est égal au quotient du côté adjacent à cet angle par l’hypoténuse.
D’où :
La longueur du segment [OI] est égal à 3,5cm. |
|
<
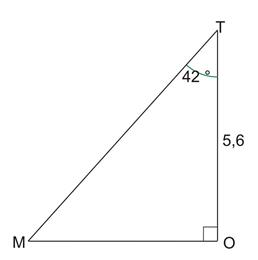
MOT est un
triangle rectangle en O tel que 
Calculer la longueur de l’hypoténuse du triangle MOT.
On sait que, MOT est un triangle
rectangle en O tel que Or, dans un triangle rectangle le cosinus d’un angle aigu est égal au quotient du côté adjacent à cet angle par l’hypoténuse.
D’où :
La longueur du segment [MT] est à peu près égale à 7,5 cm valeur approchée au dixième près par défaut. |
|
Pour calculer la mesure d’un angle aigu dans un triangle rectangle, il est nécessaire de connaître la longueur du côté adjacent à cet angle et la longueur de l’hypoténuse.
Exemple :
LAC est un triangle rectangle en C tel que LA = 5 cm et CA = 3 cm.
Calculer les mesures des deux angles aigus du triangle LAC.
On sait que, LAC est un triangle
rectangle en C tel que Or, dans un triangle rectangle le cosinus d’un angle aigu est égal au quotient du côté adjacent à cet angle par l’hypoténuse.
La mesure de l’angle aigu |
|
On sait que, LAC est un triangle
rectangle en C tel que Or, dans un triangle rectangle les angles aigus sont complémentaires. Par conséquent,
La mesure de l’angle aigu |
|
