- Le théorème de Thalès
- Utilité
- Conditions à satisfaire
- Configuration de Thalès
- Enoncé
- Exemple
Le théorème de Thalès sert à calculer une longueur.
- Un triangle dont deux côtés sont coupés par une droite parallèle au troisième côté
- Trois longueurs pour en calculer une quatrième
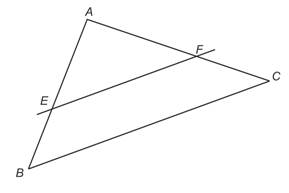
Dans un triangle, si une droite coupe deux côtés en étant parallèle au troisième côté, alors cette configuration détermine deux triangles aux côtés associés proportionnels.
Application à la configuration précédente :
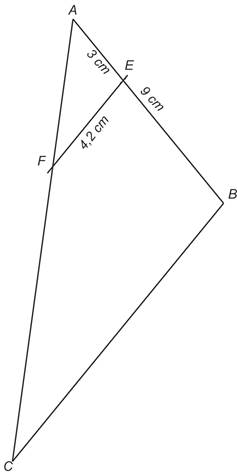
ABC est un triangle. Puisque (EF) est parallèle à (BC), les triangles AEF et ABC ont leurs côtés associés proportionnels.
![]()
ABC est un
triangle, E et F appartiennent respectivement à [AB] et [AC] et (EF) est parallèle
à (BC) ; ![]() ;
; ![]() ;
; ![]()
Calculer BC
On sait que ABC
est un triangle tel que E et F appartiennent respectivement à [AB] et [AC]
que (EF) est parallèle à (BC) et que Or, d’après le théorème de Thalès ABC et AEF ont leurs côtés associés proportionnels. D’où le tableau de proportionnalité :
La longueur du segment [BC] est égale à 12,6 cm. |
|
||||||||||||
- Agrandissement et réduction
- Définitions
- Exemple
Lorsque l’on agrandit ou que l’on réduit une figure géométrique d’un coefficient « k » :
- toutes les longueurs de ses côtés sont multipliées par « k ».
- Les figures sont alors dites semblables et leurs angles sont inchangés.
- L’orthogonalité et le parallélisme sont conservés.
![]() étant un nombre
positif, si
étant un nombre
positif, si ![]() alors il s’agit d’une réduction et si
alors il s’agit d’une réduction et si ![]() alors il s’agit d’un agrandissement.
alors il s’agit d’un agrandissement.
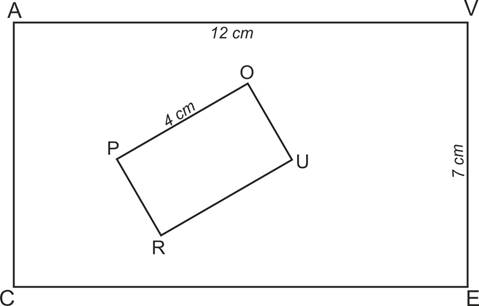
AVEC et POUR sont deux rectangles semblables, tels que ![]() ;
VE
;
VE![]() et
et ![]() .
.
- Quel est le rectangle qui est une réduction de l’autre ? Justifiez votre réponse puis calculer le coefficient de réduction.
- Calculer la longueur de [OU].
- )
- )
Les deux figures AVEC et POUR sont deux rectangles qui sont des figures semblables.
La longueur du rectangle POUR étant inférieure à celle du rectangle AVEC, on peut affirmer que POUR est une réduction de AVEC de coefficient :
![]()
![]()
![]()
Le coefficient
de réduction est ![]() .
.
Calcul de OU :
![]()
![]()
![]()
La longueur de [OU] est égale à ![]() cm.
cm.