- Définitions et vocabulaire
Une enquête statistique consiste à observer une certaine population d’individus auxquels on a décidé de s’intéresser, et à déterminer la répartition d’un certain caractère statistique dans cette population. Les informations relevées s'appellent des données.
- L’effectif d’une population est le nombre d’individus qui correspondent à la même valeur du caractère.
- L’effectif total est le nombre total d’individus d’une population étudiée.
- La fréquence est le quotient de l’effectif d’un caractère sur l’effectif total, elle est souvent exprimée en pourcentage.
- Exemple 1 : Caractère quantitatif au nombre limité de valeurs
- Le relevé statistique
- Le tableau de données
- Calcul de la fréquence de la note 15
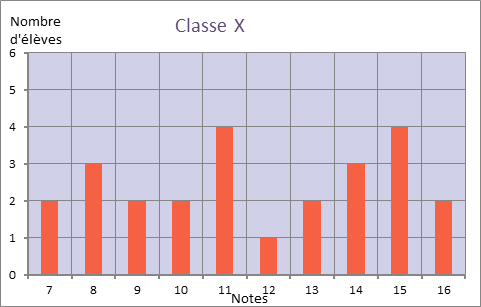
- Le diagramme en bâtons
La population étudiée est : l’ensemble des élèves d'une classe de cinquième.
Le caractère étudié est : la note (nombre entier entre 7 et 16) du devoir.
Les données sont :
12 7 15 11 9 14 8 7 11 15 11 14 9 16 13 10 15 8 13 16 11 14 8 10 15
Notes moyennes |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
total |
effectifs |
2 |
3 |
2 |
2 |
4 |
1 |
2 |
3 |
4 |
2 |
25 |
Fréquences (%) |
8,0 |
12,0 |
8,0 |
8,0 |
16,0 |
4,0 |
8,0 |
12,0 |
16,0 |
8,0 |
100,00 |
La fréquence de la note 15 est égale au quotient de l’effectif correspondant e par l’effectif total N .
![]()
![]()
![]()
![]()
La fréquence peut s’exprimer sous la forme d’un nombre décimal (<1), d’une fraction ou d’un pourcentage.
La hauteur des bâtons est proportionnelle à l’effectif correspondant à chaque note
- Exemple 2 : caractère quantitatif au différentes valeurs très nombreuses
- Le relevé statistique
- Détermination des classes
- Les représentations graphiques
La population étudiée est : Un groupe de 20 personnes.
Le caractère étudié est : Les dépenses effectuées (en €) par chacune au cours d’une sortie.
Les données brutes sont :
![]()
Toutes les valeurs étant différentes, il est nécessaires de regrouper les valeurs en ensembles appelés classes
Décidons par exemple, de constituer des classes de 25 €.
Nous pouvons alors constituer le tableau de données suivant :
Dépenses comprises |
Entre 1 et 25€ |
Entre 26 et 50€ |
Entre 51 et 75€ |
Entre 76 et 100€ |
Total |
Effectifs |
5 |
8 |
3 |
4 |
20 |
Fréquences (%) |
25 |
40 |
15 |
20 |
100 |
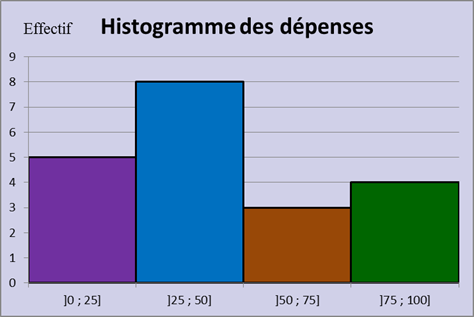
- L’histogramme
- Le diagramme circulaire
- Chaque classe est représentée par un rectangle.
- Les rectangles se touchent.
- La hauteur est proportionnelle à l’effectif.
- Chaque classe est représentée par un secteur circulaire.
- Chaque mesure d’angle de secteur est proportionnelle à l’effectifs de la classe.
- L’effectif total correspond à 360 °

Calcul de la mesure des angles des secteurs à partir d’un tableau de proportionnalité
Le coefficient de proportionnalité est :
![]()
Dépenses comprises |
]0 ; 25] |
]25 ; 50] |
]50 ; 75] |
]75 ; 100] |
Total |
|
Effectifs |
5 |
8 |
3 |
4 |
20 |
|
Mesure de l’angle (°) |
90 |
144 |
54 |
72 |
360 |
- Exemple 3 : caractère qualitatif
- Le relevé statistique
- Le tableau de données
- Les représentations graphiques
La population étudiée est : Une classe de 24 élèves.
Le caractère étudié est : Le nombre de voix obtenues par chaque candidat au cours des élections de délégué de classe.
Les données brutes du vote sont :
Mathieu – Mathieu – Anaïs – Mathieu – Anaïs – Louise – Anaïs – Mathieu – Antoine – Antoine – Mathieu – Clémentine – Mathieu – Anaïs – Anaïs – Antoine – Clémentine – Mathieu – Mathieu – Antoine – Anaïs – Anaïs – Mathieu – Antoine.
Candidat |
Anaïs |
Antoine |
Clémentine |
Louise |
Mathieu |
Total |
Effectifs (Voix) |
7 |
5 |
2 |
1 |
9 |
24 |
Fréquence (%) |
29,2 |
20,8 |
8,3 |
4,2 |
37,5 |
100 |
- Le diagramme en bâtons
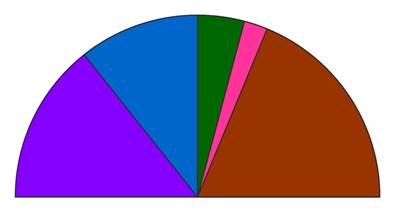
- Le diagramme semi-circulaire

On procède de la même façon qu’avec le diagramme circulaire mais à partir d’une valeur totale de 180°
Le coefficient de proportionnalité est :
![]()
Candidat |
Anaïs |
Antoine |
Clémentine |
Louise |
Mathieu |
Total |
Effectifs (Voix) |
7 |
5 |
2 |
1 |
9 |
24 |
Mesure de l’angle (°) |
52,5 |
37,5 |
15 |
7,5 |
67,5 |
180 |
|
|
|
|
|
