Proportionnalité

Reconnaitre une situation de proportionnalité d’un point de vue numérique

D’un point de vue numérique
D’un point de vue graphique

Exemples de situations de proportionnalités
Définition
Exemple 1
Exemple 2

Recette de cuisine

Ingrédients

Farine

(g)

Beurre

(g)

Œufs

(nombre)

Sucre

(g)

Levure

(paquet)

4 personnes

100

8 personnes

200

100

Changement d’unités de mesures de longueur, d’aires…

L (en cm)	200	50	8,5	2560	152,5
L (en m)	2	0,5	0,085	25,6	1,525

Agrandissement ou réduction de mesures

	Longueur	Largeur	Hanteur
Modèle réduit (cm)	14	8	5
Vrai grandeur (cm)	280	160	100

Dans un tableau de nombres de deux lignes, on a une situation de proportionnalité si chaque nombre de la première ligne est multiplié ou divisé par un même nombre pour obtenir son correspondant dans la deuxième ligne.

Ce même nombre est appelé coefficient de proportionnalité.

Soit le tableau de nombres :

4	9	18
6	13,5	27

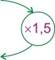
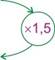
Calculs des quotients :

Conclusion :

Les quotients sont égaux, c’est une situation de proportionnalité.

Le coefficient de proportionnalité est 1,5

4	9	18
6	13,5	27

Soit le tableau de nombres :

10	9	5
6	5,4	2,9

Calculs des quotients :

Conclusion :

Les quotients ne sont pas égaux, ce n’est pas une situation de proportionnalité.

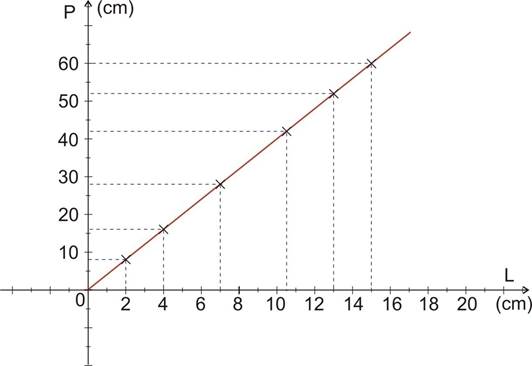
Graphiquement, on reconnait une situation de proportionnalité lorsque les points sont alignés sur une droite passant par l’origine de repère.

Remarque :

Les points ont pour coordonnées en abscisse un nombre de la première ligne du tableau et pour ordonnée, son correspondant dans la deuxième ligne.

Exemple 1 : proportionnalité
Exemple 2 : non-proportionnalité
Exemple 3 : non-proportionnalité

Longueur du côté L (cm)	2	4	7	10,5	13	15
Périmètre du carré P (cm)	8	16	28	42	52	60

Longueur du côté L (cm)	2	3	5	8	10	12
Aire du carré A (cm²)	4	9	25	64	100	144

Nombres de séances (N)	2	5	10	15	20
Prix (P)	20	35	60	85	110

Propriétés des tableaux de proportionnalité

Situation de quatrième proportionnelle.
Multiplication (et division)
Addition (et soustraction)

Dans une situation de quatrième proportionnelle, quatre nombres sont supposés proportionnels, on calcule la valeur de l’un en connaissant la valeur des trois autres.

Exemple

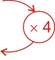
12	x
4	2,5

Si on multiplie ou divise les deux nombres d’une colonne par un même nombre, alors on obtient les deux nombres d’une autre colonne du tableau de proportionnalité.

Exemple

4	9	18
6	13,5	27

Déterminer de nouvelles colonnes dans le tableau de proportionnalité précédent

4	4 × 3	9	18	18 ÷ 3
6	6×3	13,5	27	27 ÷ 3

4	12	9	18	6
6	18	13,5	27	9

Vérification :

Si on ajoute ou soustrait d’une part les deux nombres d’une même ligne puis d’autre part leurs correspondants dans la deuxième ligne, on obtient deux nombres d’une autre colonne du tableau de proportionnalité.

Exemple

4	9	18
6	13,5	27

Déterminer de nouvelles colonnes dans le tableau de proportionnalité précédent

4	9	4 + 9	18	18 – 4
6	13,5	6 + 13,5	27	27 – 6

4	9	13	18	14
6	13,5	19,5	27	21

Vérification :

Situations de proportionnalité particulières

Échelle
Calcul d’un pourcentage

L’échelle d’une représentation graphique est égale au quotient de la longueur reproduite par la longueur réelle, c’est le coefficient de proportionnalité qui permet de passer des mesures réelles à celles de la représentation.

Exemple :

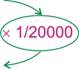
Le plan d’une ville est une réduction de la réalité son échelle est inférieure à 1.

Par exemple (écrit souvent 1/20 000 sur les plans)

Longueur réelle L (en cm)	20 000	10 000	240 000	500 000	60 000
Longueur sur le plan l (en cm)	1	0, 5	12	25	3

Un pourcentage est le coefficient de proportionnalité d’une situation, il est exprimé sous la forme d’un quotient dont le dénominateur est cent.

Exemple :

Dans une classe de cinquième de 20 élèves, il y a 3 élèves sur cinq qui sont des filles.

On peut aussi l’écrire : 6 élèves sur 10 sont des filles ou bien 60% des élèves de cette classe de cinquième sont des filles.

60% est un pourcentage, qui se lit « 60 pour 100 » et qui s’écrit