La géométrie dans l'espace consiste à étudier des objets dans un espace à trois dimensions.
Les objets de l’espace s’appellent des solides.
- Prismes droits
- Définitions
- Cas particuliers
- Patrons
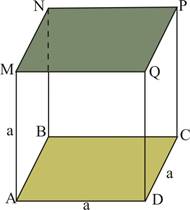
Un prisme droit est composé de :
- deux bases polygonales parallèles et superposables
- faces latérales rectangulaires, perpendiculaires aux bases et du même nombre que celui des côtes des bases
Exemple : le pentagone : Il possède 7 faces : § 2 bases qui sont des pentagones identiques § 5 faces latérales qui sont des rectangles |
|
Remarque :
La hauteur est la longueur commune des arêtes latérales
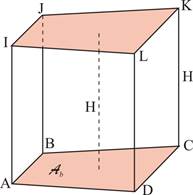
Pavé |
Cube |
Prisme droit à base triangulaire |
|
|
|
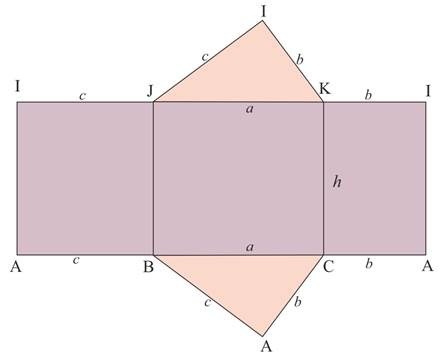
- Prisme droit à base triangulaire
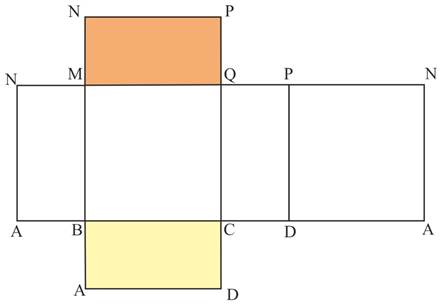
- Parallélépipède rectangle
- Cylindres
- Définition
- Patron
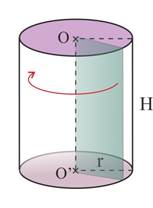
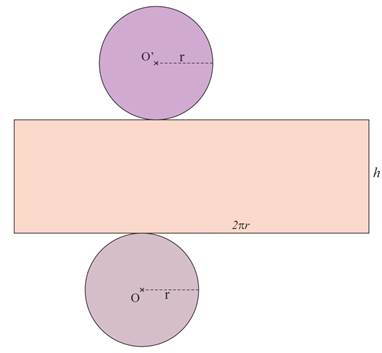
Un cylindre est engendré par un rectangle faisant une révolution autour d’un de ses côtés (axe du cylindre) |
|
Un cylindre est composé de :
|
|
- La perspective cavalière
Les perspectives permettent de représenter un solide qui est en trois dimensions sur un support en deux dimensions en donnant l’impression visuelle des trois dimensions (3D)
- Règles de perspective cavalière
- Prisme droit
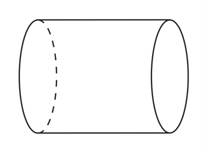
- Cylindre
Dans une représentation en perspective cavalière :
- Toutes les droites parallèles restent parallèles sur le dessin.
- Les arêtes cachées sont représentées en pointilles.
- Les parties du solide qui sont vues exactement de face (en général la face avant) sont en vraie grandeur sur le dessin..
- Les égalités de longueurs sont conservées.
|
|
Les disques des bases ne sont pas perpendiculaires au regard et sont donc déformées. Ils deviennent ovales. |
|