|
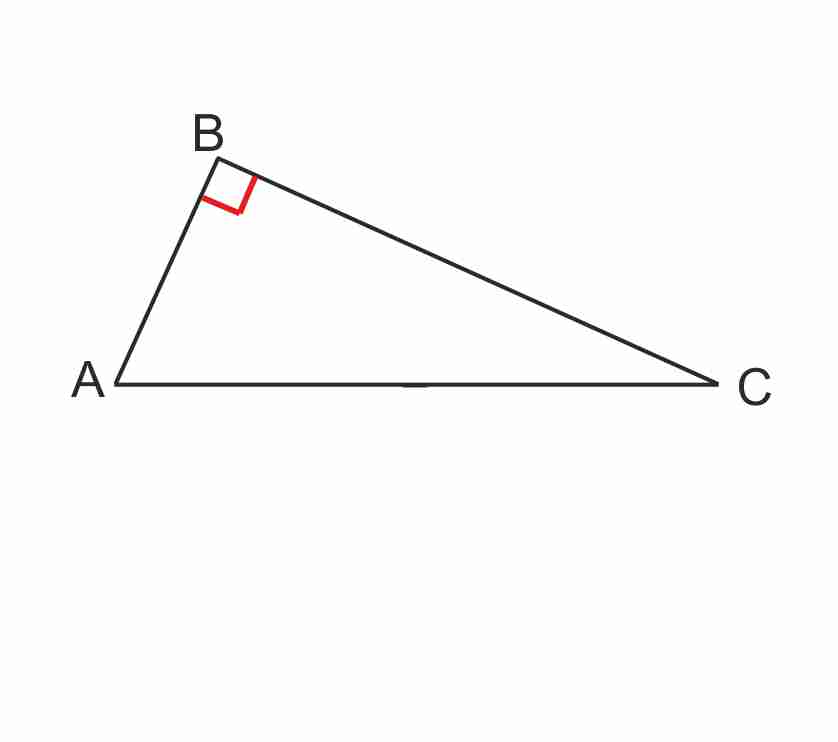
Un triangle rectangle est un triangle qui possède un angle droit, et deux angles (aigus) complémentaires. Le côté opposé à l’angle droit s’appelle l’hypoténuse. |
|
- Propriétés directes
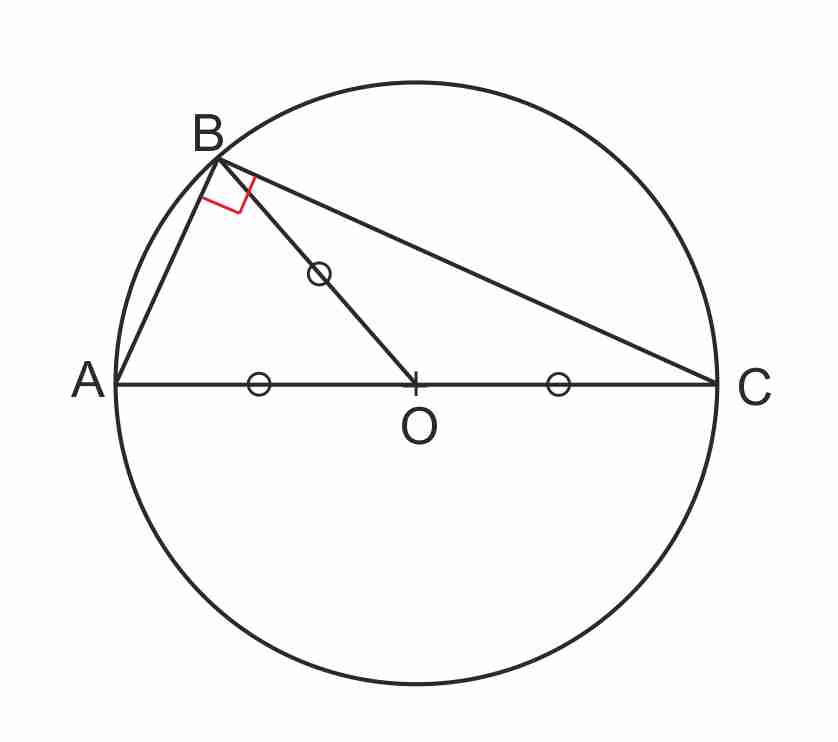
- Si un triangle est rectangle, alors son cercle circonscrit a pour centre le milieu de son hypoténuse.
- Si un triangle est rectangle, alors le milieu de l’hypoténuse est équidistant des trois sommets.
- Si un triangle est rectangle, alors son hypoténuse est un diamètre de son cercle circonscrit.
- Si un triangle est rectangle, alors la médiane issue du sommet de l’angle droit a pour longueur la moitié de celle de son hypoténuse.
Si |
- Propriétés réciproques
- Propriété 1
- Propriété 2
- Propriété 3
- Propriété 4
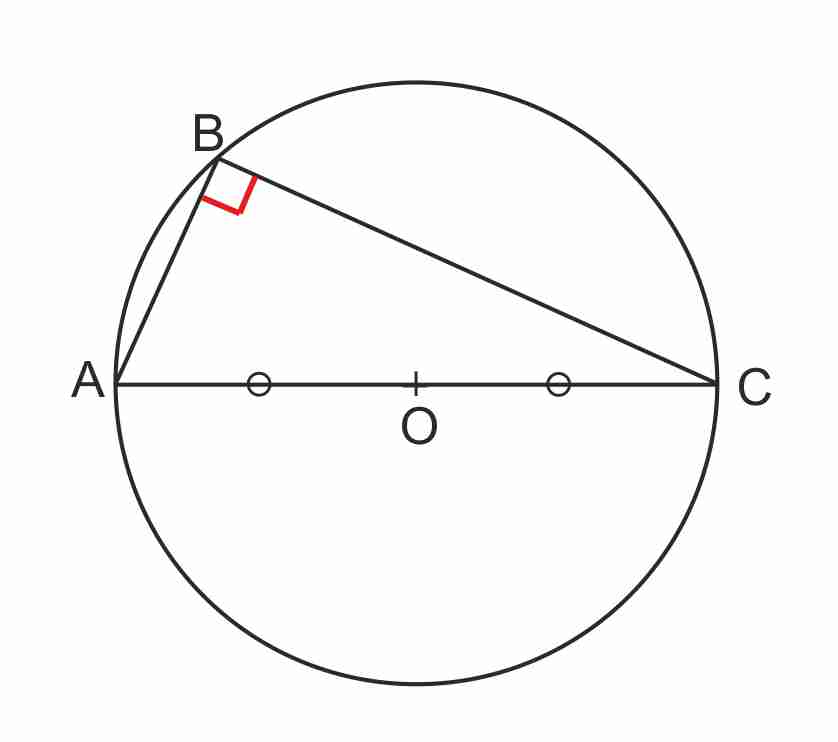
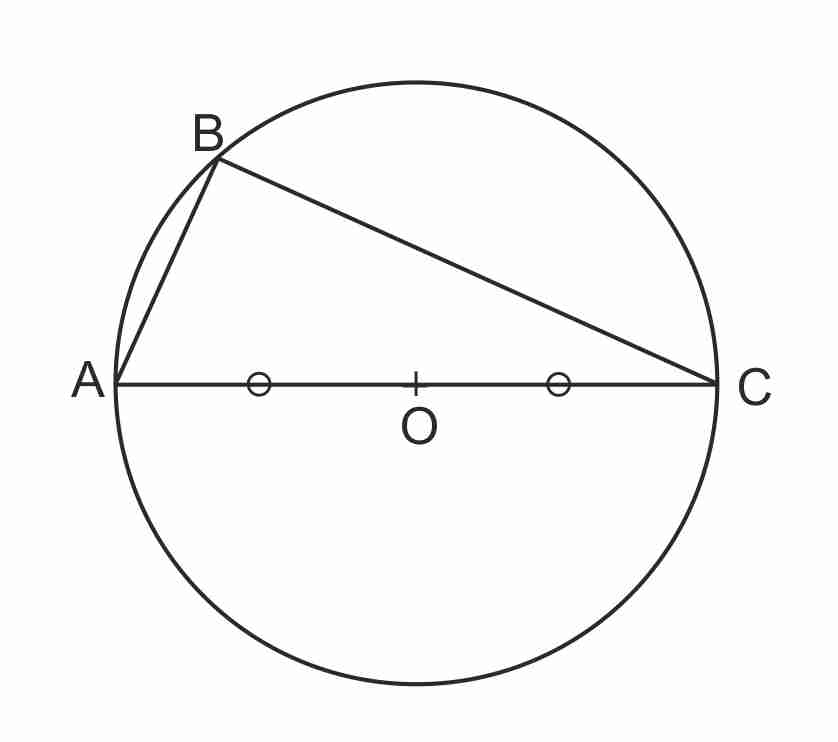
Si un triangle est inscrit dans un cercle (demi-cercle) ayant pour diamètre un côté alors ce triangle est rectangle.
Si |
Si ABC est inscrit dans un cercle de diamètre [AC], alors ABC est un triangle rectangle en B |
Si le milieu d’un côté d’un triangle est équidistant des trois sommets alors ce triangle est rectangle.
Si |
Si le milieu O du côté [AC] est équidistant des trois sommets A, B, C, alors ABC est un triangle rectangle en B |
Si le milieu d’un côté d’un triangle est le centre de son cercle circonscrit alors ce triangle est rectangle.
Si |
Si le milieu O du côté [AC] est le centre du cercle circonscrit à ABC, alors ABC est un triangle rectangle en B |
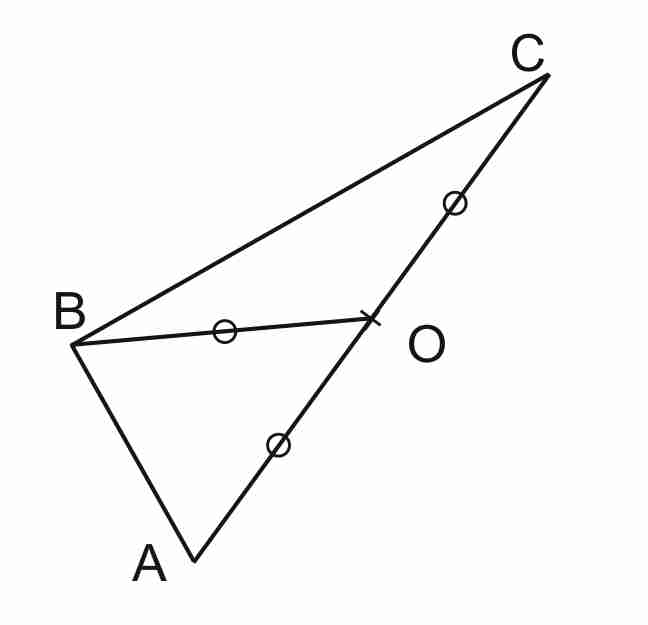
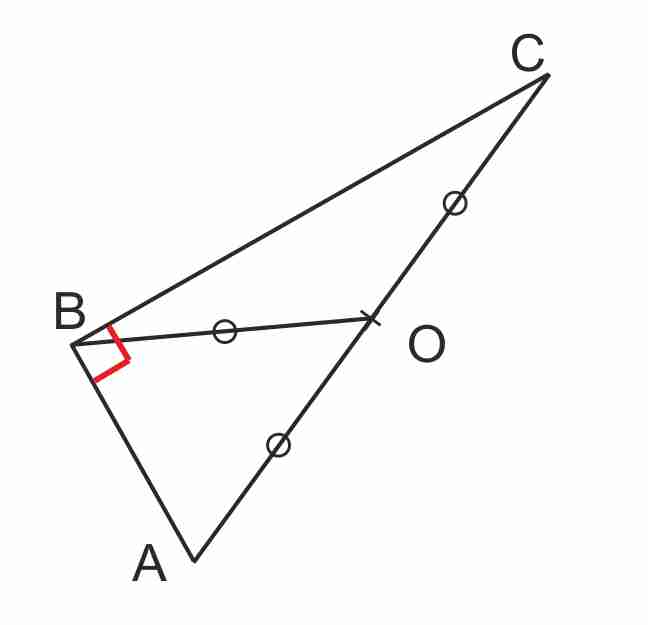
Dans un triangle, si la longueur de la mediane relative à un côté est égale à la moitié de la longueur de ce côté alorsle triangle est rectangle.
Si |
Si la longueur de la mediane [BO] est égale à la moitié du côté [AC], alors ABC est un triangle rectangle en B |