- Le théorème de Pythagore
- Utilité
- Conditions d’utilisation
- Énoncé
- Applications
Le théorème de Pythagore sert à calculer la longueur d'un côté d’un triangle rectangle.
Il faut réunir les conditions suivantes :
- Un triangle rectangle.
- Connaitre les longueurs de deux côtés de ce triangle.
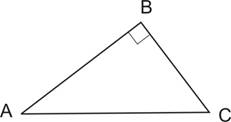
Si un triangle est rectangle, alors le carré de son hypoténuse est égale à la somme des carrés des deux côtés de l’angle droit.
- Calcul de l’hypoténuse
- Calcul d’un côté de l’angle droit
Exercice
CIA est un triangle rectangle en C tel que CI = 3,3 cm et CA = 4,4cm.
Calculer la longueur de [AI].
On sait que CIA est un triangle rectangle en C et que CI = 3,3 cm et CA = 4,4cm.
Par conséquent, d’après le théorème de Pythagore :
Donc, la longueur de [AI] est 5,5 cm.
Exercice
KGB est un triangle rectangle en K tel que GB = 4,5 cm et KG = 2,7cm.
Calculer la longueur de [KB].
On sait que KGB est un triangle rectangle en K et que GB=4,5 cm et KG=2,7cm.
Par conséquent, d’après le théorème de Pythagore
Donc, la longueur de [KB] est 3,6 cm.
- La réciproque du théorème de Pythagore.
- Utilisation
- Enoncé de la réciproque
- Application
La réciproque du théorème de Pythagore sert à démontrer qu’un triangle est rectangle en connaissant les longueurs de ses trois côtés.
Dans un triangle, si le carré du plus grand côté est égal à la somme des carrés des deux autres côtés alors ce triangle est rectangle.
RSF est un triangle tel que RS = 4 cm ; RF = 5 cm et FS = 3 cm.
Est-ce que le triangle RSF est un triangle rectangle ?
On sait que dans le triangle RSF, RS = 4 cm ; RF = 5 cm et FS = 3 cm.
On calcule :
d’une part :
et d’autre part :
Par conséquent :
Donc, d’après la réciproque du théorème de Pythagore RSF est un triangle rectangle en S.
- La contraposée du théorème de Pythagore
- Utilisation
- Énoncé de la contraposée
- Application
La contraposée du théorème de Pythagore sert à démontrer qu’un triangle n’est pas rectangle en connaissant les longueurs de ses trois côtés.
Dans un triangle, si le carré du plus grand côté n’est pas égal à la somme des carrés des deux autres côtés alors ce triangle n’est pas rectangle.
FIP est un triangle tel que FI = 4,5 cm ; IP=5,9 cm et FP = 7,5 cm.
Est-ce que le triangle FIP est un triangle rectangle ?
On sait que dans le triangle FIP, FI = 4,5 cm ; IP = 5,9 cm et FP = 7,5 cm.
On calcule :
d’une part :
et d’autre part :
Par conséquent :
Donc, d'après la contraposée du Théorème de Pythagore, FIP n’est pas un triangle rectangle.
et se lit "racine carré de 30,25"
pour obtenir la valeur exacte ou approchée