Prouver qu'un quadrilatère est un parallélogramme

Construction du triangle EFG

Calcul de la mesure de l'angle

Dans un triangle, la somme des angles est égale à 180°, donc :

Construction du triangle EGH :

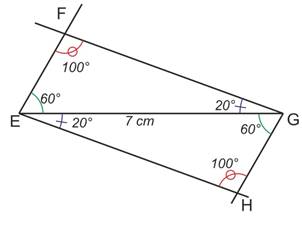
Prouver que EFGH est un parallélogramme

Donc

Dans le triangle EGH, on calcule comme précédemment la mesure de l’angle

Donc

Par conséquent, la quadrilatère EFGH a ses angles opposés de même mesure.

Or, si un quadrilatère a ses angles opposés de même mesure, alors c’est un parallélogramme.

Donc, EFGH est un parallélogramme.