- Figures symétriques
- Définition
- Symétrique d’un point
- Construction du symétrique d’un point
- F et F' sont symétriques par rapport à la droite (d).
- F est le symétrique de F’ par rapport à l’axe (d).
- F’ est le symétrique de F par rapport à l’axe (d).
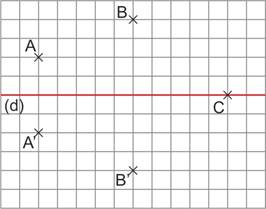
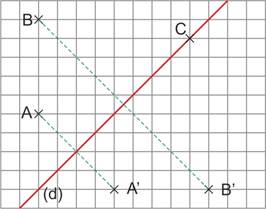
- En utilisant un quadrillage
- En utilisant une équerre et une règle graduée
- En utilisant un compas et une règle
- Etape 1
- Etape 2
- Etape 3
- Etape 4
- Etape 5
- Etape 6
- Etape 7
- Etape 8
- Etape 1
- Etape 2
- Etape 3
- Etape 4
- Etape 5
- Etape 6
- Etape 7
- Etape 8
- Propriétés de la symétrie axiale
- Points alignés
- Segments
- Angles
- Cercles
- Aires et des périmètres
- Conclusions
- L’alignement des points.
- Les longueurs des segments.
- Les mesures des angles.
- Les aires.
- Les natures des figures géométriques.
Deux figures sont symétriques par rapport à une droite si elles se superposent par pliage le long de cette droite. Cette droite s’appelle un axe de symétrie.
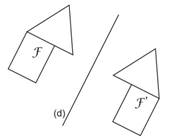
On dit que :
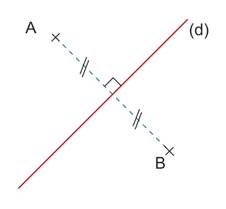
Si deux points sont symétriques par rapport à une droite alors, cette droite est la médiatrice du segment qui a pour extrémités ces deux points.
|
Si A
et B sont symétriques par rapport à (d) |
|
|
A’ est le symétrique de A par rapport à (d)
B’ est le symétrique de B par rapport à (d)
C’ est le symétrique de C par rapport à (d)
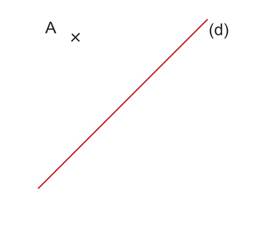
Construite le symétrique de A par rapport à (d) avec une équerre et une règle graduée.
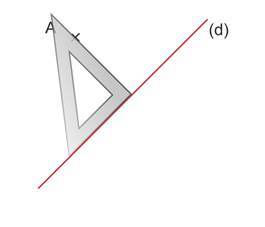
Placer l’équerre le long de (d) et la faire glisser jusqu’au point A
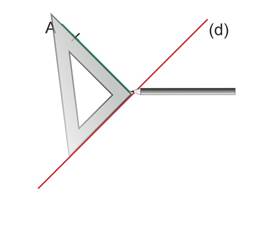
Tracer la droite le long de l’équerre
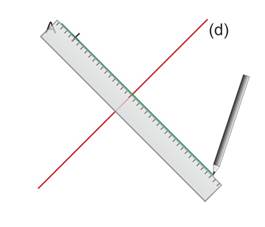
Prolonger la droite au-delà de (d) à l’aide d’une règle.
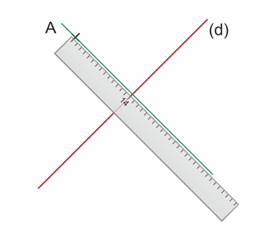
Mesurer la distance de A à (d), ici 14
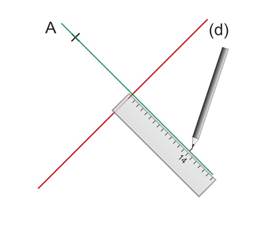
Reporter cette distance sur la droite de l’autre côté de (d)
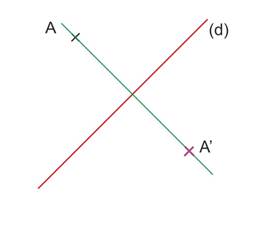
Nommer le point obtenu
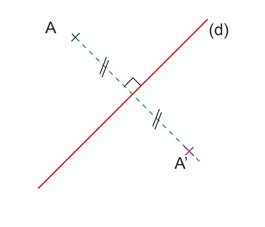
A’ est bien le symétrique de A par rapport à (d)
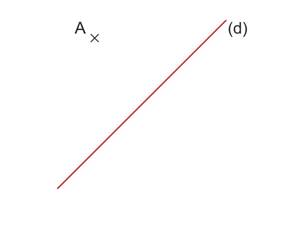
Construite le symétrique de A par rapport à (d) avec un compas.
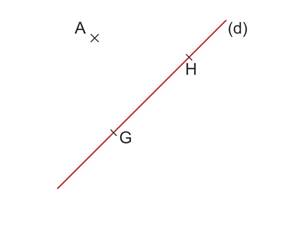
Placer deux points G et H sur la droite (d).
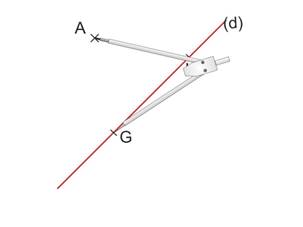
Piquer le compas en G et prendre pour ouverture la distance GA.
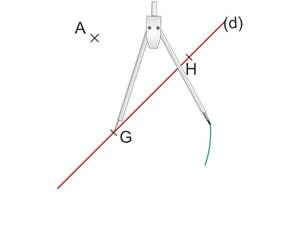
Tracer un arc de cercle de l’autre côté de (d).
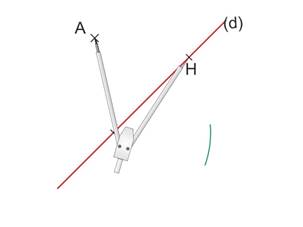
Piquer le compas en H et prendre
pour ouverture la distance HA.
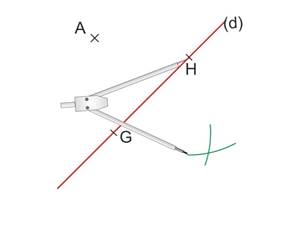
Tracer un deuxième arc de cercle coupant le premier.
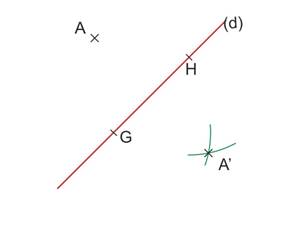
Nommer l’intersection, il s’agit du symétrique de A par rapport à la droite (d)
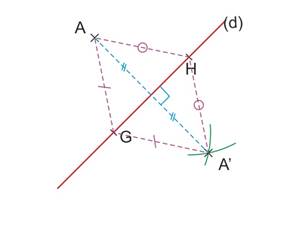
(d) est la médiatrice du segment [AA’]
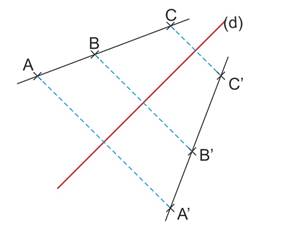
Les symétriques de points alignés sont alignés
Remarque :
Cela signifie que le symétrique d'une droite par symétrie axiale est une droite
|
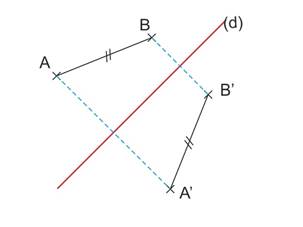
Si A’ est le symétrique de A et C’ le symétrique de C, alors le symétrique de la droite (AC) est la droite (A’C’) |
Le symétrique d'un segment est un segment de même longueur
|
Si [A'C'] est le symétrique de [AC], |
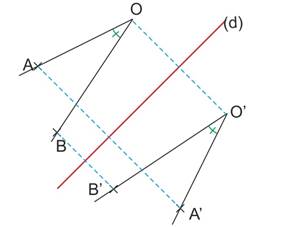
Le symétrique d'un angle est un angle de même mesure.
|
Si |
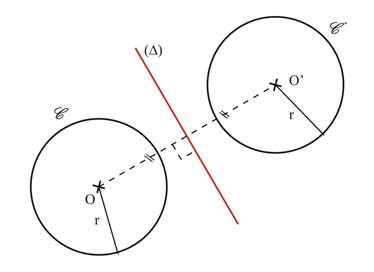
Le symétrique d'un cercle est un cercle de même rayon.
|
Si C et C’sont symétriques, alors leurs centres O et O’ sont symétrique et ils ont même rayon |
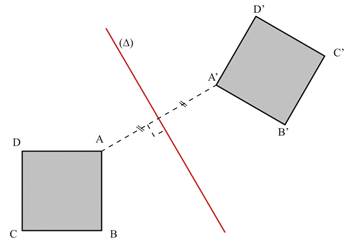
Deux figures symétriques ont la même aire et les mêmes périmètres
|
Si ABCD et A’B’C’D’ sont symétriques, alors Aire(ABCD)= Aire(A’B’C’D’) et Périmètre(ABCD) = Périmètre(A’B’C’D’) |
D’une façon générale ont dit que la symétrie axiale conserve :