- Définitions, vocabulaire notations
- Droites sécantes
- Droites concourantes
- Droites perpendiculaires
- Droites parallèles
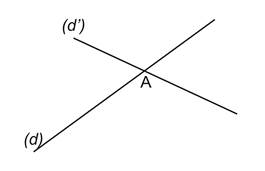
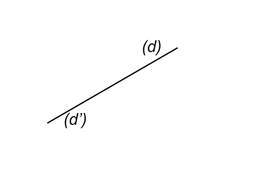
Deux droites sécantes sont deux droites qui se coupent en un point.
(d) et (d') sont sécantes en A. A est le point d'intersection |
|
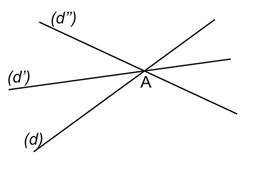
Des droites (plus de deux) concourantes sont des droites qui se coupent en un point.
(d), (d') et (d'') sont concourantes en A. A est le point de concours |
|
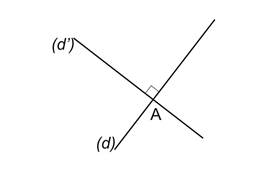
Deux droites perpendiculaires sont deux droites sécantes qui forment un angle droit.
(d) et (d') sont perpendiculaires en A. |
|
Notation :
(d) « est perpendiculaire à » (d') se note :
![]()
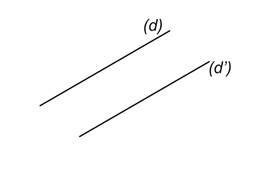
Deux droites parallèles sont deux droites qui n'ont aucun point en commun, on dit alors, qu'elles sont strictement parallèles, ou qui ont tous leurs points en commun, dans ce cas on dit qu'elles sont confondues.
(d) et (d') sont deux droites strictement parallèles |
(d) et (d') sont deux droites parallèles et confondues. |
Notation :
(d) est parallèle à (d') se note :
(d) // (d')
- Propriétés euclidiennes
- Axiomes d'Euclide
- Propriétés
Un axiome est une proposition évidente, dont la vérité est reconnue sans démonstration.
- Avec un point
- Avec deux points
- Avec un point et une droite
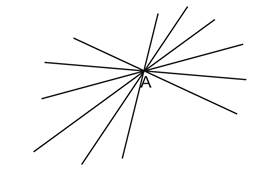
Par un point passe une infinité de droites. |
|
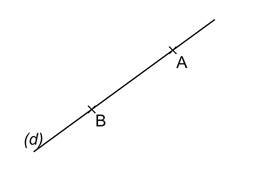
Par deux points passe une et une seule droite. |
|
|
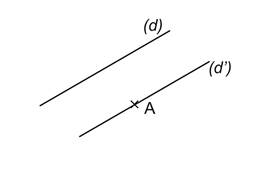
Par un point il passe une parallèle et une seule à une droite.
|
|
- Deux droites parallèles à une troisième
- Deux droites sont perpendiculaires à une troisième droite
- Une parallèle à une de deux droites perpendiculaires
- Une perpendiculaire à deux droites perpendiculaires
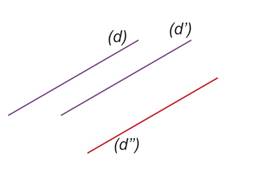
Si deux droites sont parallèles à une troisième droite, alors elles sont parallèles.
Si |
|
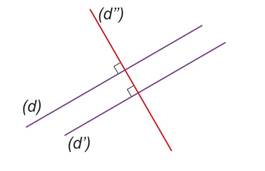
Si deux droites sont perpendiculaires à une troisième droite, alors elles sont parallèles.
Si |
|
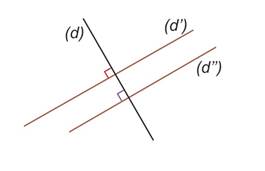
Si deux droites sont perpendiculaires, toute droite parallèle à l'une est alors perpendiculaire à l'autre.
Si |
|
Si deux droites sont perpendiculaires, toute droite perpendiculaire à l'une est alors parallèle à l'autre.
Si |
|
- Constructions avec une équerre
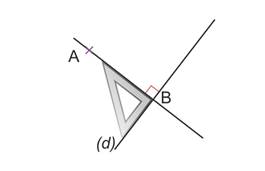
- d'une perpendiculaire à une droite passant par un point
- de deux droites parallèles
(AB) est perpendiculaire à (d') et passe par A. |
|
Cliquer ici pour voir l'animation de la construction
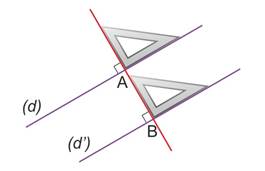
On peut construire deux droites parallèles, en utilisant une équerre et la propriété suivante :
Si deux droites sont perpendiculaires à une troisième, alors elles sont parallèles.
Puisque (d) et (d') sont perpendiculaires à (AB), alors (d) et (d') sont parallèles. |
|
Cliquer ici pour voir l'animation de la construction