- Définitions, vocabulaire et notations
- Vocabulaire
- Définition
- Notation et différentes écritures
Les chiffres permettent d’écrire tous les nombres, ils sont au nombre de dix :
Exemple :
|
est un chiffre |
|
sont des nombres |
|
est aussi un nombre |
Un nombre décimal est composé de deux parties séparées par une virgule.
De part et d’autre de la virgule, à gauche, se trouve la partie entière et à droite, la partie décimale.
Exemple :
980,14 980 0,14 |
est un nombre décimal est la partie entière est la partie décimale |
Une nombre décimal (n) est écrit comme la somme de sa partie entière (a) et de sa partie décimale (b).
Exemple :
|
est un nombre décimal. |
|
|
|
Remarque
Un nombre entier est un est un nombre décimal dont la partie décimale est égale à zéro.
- Ecriture en chiffres
- Ecriture en lettres
- Ecriture décimale décomposée
- Ecriture fractionnaire
La position d’un chiffre dans un nombre détermine sa signification.
Exemple :
|
est un nombre décimal. signifie une dizaine. signifie cinq unités signifie trois centièmes |
Dans ce nombre 15,732 le nombre de dixièmes est 157.
En utilisant le tableau ci-dessous, on visualise le sens de la position respective de chaque chiffre dans un nombre décimal.
Partie entière |
virgule |
Partie décimale |
||||||
Dix mille |
mille |
centaine |
dizaine |
unité |
dixième |
centième |
millième |
|
1 |
5 |
, |
7 |
3 |
2 |
|||
Remarque :
Les zéros situés à gauche de la partie entière et ceux à droite de la partie décimale peuvent être enlevés ou ajoutés en fonction de leur utilité.
Exemple :
Orthographe :
- mille est invariable, mais millier, million, milliard… s’accordent
- Dans la partie entière et dans la partie décimale, cent de quatre-vingt sont invariables s’ils sont suivis d’autres chiffres.
- Tous les mots qui composent un nombre peuvent être séparés (de préférence) ou non par un trait d’union.
Exemples :
 s’écrit Mille-huit-cents.
|
Cent prend un s |
 s’écrit trois-mille-cinq-cent-quatre-vingts.
|
Cent est invariable mais pas vingt |
|
Cent et vingt sont invariables ici |
|
Vingt prend un s |
|
Vingt est invariable ici |
s’écrit quatre-mille-deux-cent-quatre-vingt-trois
s’écrit 
s’écrit
Exemple :
Exemple :
- Représentation des nombres décimaux sur une droite graduée
- Demi-droite graduée
- Abscisse d’un point
Une demi-droite graduée fait apparaitre une graduation régulière qui doit correspondre à un partage en un nombre de parts égales.
L’extrémité de la droite correspond au zéro de la graduation. On indique ensuite l’unité qui permettra le repérage précis d’un point.
Chaque point d’une demi-droite graduée est repéré par un nombre qui s’appelle l’abscisse de ce point.
Notation
Le point C d’abscisse 3 se note C
.
Changement d’échelle :
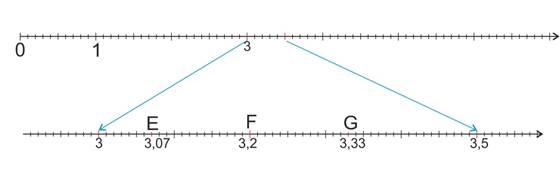
- Comparaison de nombres décimaux
- Comparer
- Ranger
- Encadrer-intercaler
- Valeurs approchées
Comparer deux nombres, c’est préciser si ces deux nombres sont égaux ou différents.
Si les deux nombres sont différents, on pourra dire quel est celui qui est supérieur ou inférieur à l’autre.
Notations :
On peut utiliser les symboles suivants en comparant deux nombres :
« 
» qui
signifie « est égal à »
« 
»
qui signifie « est différent de »
« 
»
qui signifie « est à peu près égal à »
« 
»
qui signifie « est supérieur à »
« 
»
qui signifie « est inférieur à »
Exemples :
Ranger des nombres dans ordre croissant, c’est les ranger du plus petit au plus grand.
Ranger des nombres dans ordre décroissant, c’est les ranger du plus grand au plus petit.
Exemples :
Ranger dans l’ordre croissant les
nombres 
, ces
nombres sont rangés dans ordre croissant.
Ranger dans l’ordre décroissant les
nombres 
, ces
nombres sont rangés dans ordre décroissant.
Encadrer un nombre entre deux autres, c’est écrire un nombre plus petit et un nombre plus grand que ce nombre.
Exemples :
est encadré par 
et 
Intercaler un nombre entre deux autres, c’est écrire un nombre compris entre ces deux nombres.
Exemple :
Entre et ,
on peut intercaler
- Une valeur approchée par défaut, est une valeur proche du nombre mais plus petite.
- Une valeur approchée par défaut d’un nombre est appelée une troncature de ce nombre.
- Une valeur approchée par excès, est une valeur proche du nombre mais plus grande.
- Celle des deux valeurs approchées d’un nombre qui est la plus proche de celui-ci est appelée un arrondi de ce nombre.
Exemple :
,
c’est une valeur approchée de 
au centième près par défaut.
Exemple :
0,73 est une troncature de
Exemple :
,
c’est une valeur approchée de au centième près par excès.
Exemple :
0,73 est un arrondi de au
centième près par défaut.
0,74 est un arrondi de 0,737 au centième près par excès.