- Périmètre
- Périmètres de polygones
- Périmètre d’un cercle
- Le périmètre d’un triangle
- Le périmètre d’un rectangle
- Le périmètre d’un carré
- Aire
- Mesure des aires
- Aires de polygones
- Aire du disque
- L'aire d’un carré
- L'aire d’un rectangle
- L'aire d’un triangle rectangle
- Volume
- Mesure des volumes
- Volume d’un parallélépipède rectangle
- Volume d’un cube
Le périmètre d’une figure géométrique est la mesure du contour de la figure.
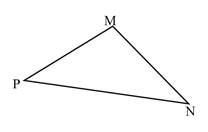
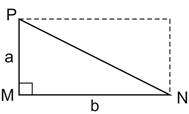
Le périmètre d’un triangle est égal à la somme des longueurs de ses trois côtés.
|
Le périmètre du triangle MNP est :
|
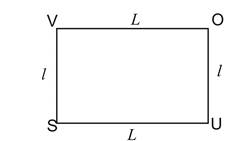
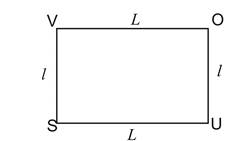
Le périmètre d’un rectangle est égal à la double somme de sa longueur et de sa largeur ou la somme du double de sa longueur et du double de sa largeur.
|
Le périmètre du rectangle VOUS est :
ou
|
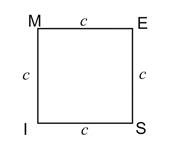
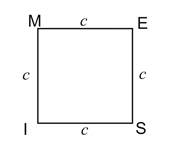
Le périmètre d’un carré est égal au quadruple de la longueur du côté.
|
Le périmètre du carré MESI est :
|
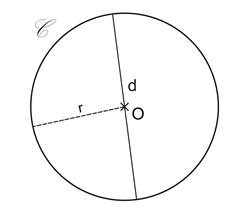
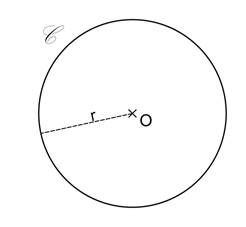
Le périmètre d’un cercle s’appelle la circonférence du cercle, il est égal au produit de la longueur de son diamètre par le nombre π ou le double produit de la longueur de son rayon par π.
|
Le périmètre du cercle C est :
ou
|
π est le quotient exact de la circonférence d’un cercle par la longueur de son diamètre
Sa valeur approchée par défaut est 3,14
L’aire d’une figure géométrique est la mesure de la surface délimitée par cette figure.
|
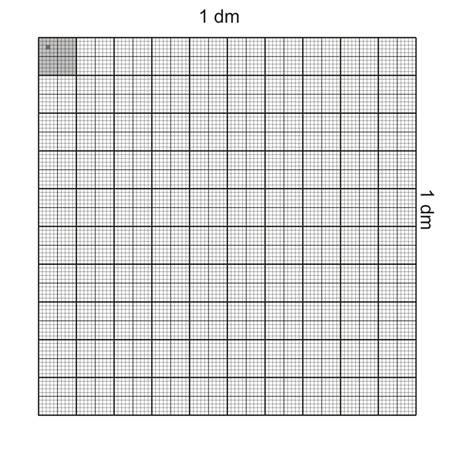
Un carré de 1 dm de côté contient 100 carrés de 1 cm de côté
Un carré de 1 cm de côté contient 100 carrés de 1 mm de côté
Un carré de 1 dm de côté contient 10 000 carrés de 1 mm de côté
|
kilomètre carré |
hectomètre carré |
décamètre carré |
mètre carré |
décimètre carré |
centimètre carré |
millimètre carré |
|||||||
|
|
|
|
|
|
|
|||||||
0, |
0 |
0 |
1 1 1 |
2, 2 2 |
3 3 3 |
0, |
|||||||
![]()
Voir la fiche. La virgule doit être déplacée de deux rangs en deux rangs
L’aire d’un carré est égale au produit de la longueur du côté par lui-même.
|
L’aire du carré MESI est :
ou
|
L’aire d’un rectangle est égale au produit de sa longueur par sa largeur.
|
L’aire du rectangle VOUS est :
|
L’aire d’un triangle rectangle est égale à la moitié du produit des longueurs des côtés de l’angle droit.
|
L’aire du triangle MNP est :
|
L’aire d’un disque est égale au produit de π par le carré du rayon de ce disque
|
L’aire du disque C est :
ou
|
Le volume d’une figure géométrique est la mesure de l’espace à l’intérieur du contour de la figure.
Dans un cube de 1 dm de côté on trouve 1000 cubes de 1 cm de côté
![]()
![]()
L’unité de volume est le mètre cube noté m3. L’unité de contenance est le litre, noté L. |
|
kilomètre cube |
hectomètre cube |
décamètre cube |
mètre cube |
décimètre cube |
centimètre cube |
millimètre cube |
||||||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
hL |
daL |
L |
dL |
cL |
mL |
|
|
|
|
|
|
|
|
0, |
0 |
4 4 4 |
5, 5 5 |
3 3
|
0 |
0, |
|
|
|
|
|
|
|
|
|
![]()
La virgule doit être déplacée de trois rangs en trois rangs
Pour les unités de contenance, les conversions se font rang par rang
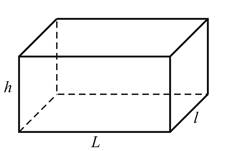
Le volume d’un parallélépipède rectangle est égal au produit de l’aire de la base par la hauteur.
Il est égale au produit de ses trois dimensions (les deux dimensions de sa base : sa longueur et sa largeur et de sa hauteur).
|
Le volume du parallélépipède rectangle est :
ou
|
Ab représente l’aire de la base h représente la hauteur du prisme |
L la longueur de la base l la largeur de la base |
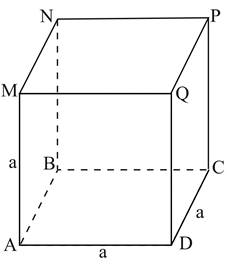
Le volume d’un cube est égal au produit de trois facteurs égaux à la longueur de son arête.
|
Le volume du cube est :
ou
|