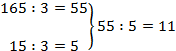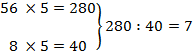- Généralités
- Définitions, vocabulaire et notation
- Remarques
- Le reste est toujours inférieur au diviseur.
- Si le reste est égal à 0, le résultat de la division est le quotient exact
- Le dividende est la somme du produit du quotient par le diviseur, et du reste.
- Le diviseur est un nombre différent de zéro.
- Multiples et diviseurs
- Exemples de multiples et de diviseurs
- Critères de divisibilité
- Un nombre est divisible par deux s’il est pair :
- Un nombre est divisible par trois si la somme de ses chiffres est un multiple de trois
- Un nombre est divisible par quatre si le nombre constitué par ses deux derniers chiffres est divisible par 4 :
- Un nombre est divisible par de cinq si son chiffre des unités est zéro ou cinq :
- Un nombre est divisible par neuf si la somme de ses chiffres est neuf
- Propriétés
- Diviser par 10 , 100 ou 1000
- Diviser par 0,1 ; 0,01 ; 0,001.
- Un quotient ne change pas
- Divisions décimales posées
- Avec deux nombres entiers
- Etape 1
- Etape 2
- Etape 3
- Etape 4
- Etape 5
- Etape 6
- Avec deux nombres à virgules
- Etape 1
- Etape 2
- Etape 3
- Etape 4
- Etape 5
- Etape 6
Un quotient est le résultat d’une division.
Le dividende est le nombre qui est divisé.
Le diviseur est le nombre qui divise.
Diviser, c’est calculer combien de fois il y a le nombre diviseur, dans le nombre dividende.
Exemple :
;
1 est le reste
Il y a 3 fois 12 dans 37.
3 est le quotient entier de 37 par 12.
37 est le dividende, 12 est le diviseur.
Le reste est la différence entre le dividende est le produit du quotient par le diviseur.
Une division euclidienne est une division dont le dividende, le diviseur, le quotient et le reste sont des nombres entiers.
3 est le quotient entier de 36 par 12
36 est un multiple de 3 parce que 
.
On peut dire aussi que 36 est un multiple de 12.
3 est un diviseur de 36 parce que 
(quotient exact)
On peut dire aussi que 12 est un diviseur de 36.
36 est un multiple de 3 alors, on peut dire que 36 est divisible par 3.
De la même façon, 36 est aussi divisible par 12.
Remarque :
Les multiples et les diviseurs sont des nombres entiers.
1234 est un multiple de 2 car il est pair. (
)
234 est un multiple de trois car 2 + 3 + 4 = 9
7744 est un multiple de 4 car 44 est divisible par 4
1745 est un multiple de 5 car il se termine par 5
14920 est un multiple de 5 car il se termine par 0
24 507 est un multiple de neuf car 2 + 4 + 5 + 7 = 18.et 1 + 8 = 9
Si on divise un nombre par 10, 100 ou 1000…, on décale vers la gauche sa virgule du même nombre de rang que celui des zéros dans les nombres, 10, 100 ou 1000.
Remarque :
Cela revient à multiplier par 0,1 ; 0,01 ; 0,001.
Exemples :
2 rangs |
1 rang |
3 rangs |
Si on divise un nombre par 0,1 ; 0,01 ; 0,001…, on décale vers la droite sa virgule du même nombre de rang que celui des chiffres après la virgule dans les nombres 0,1 ; 0,01...
Remarque :
Cela revient à multiplier par 10 ; 100 ou 1000.
Exemples :
2 rangs |
1 rang |
3 rangs |
Un quotient ne change pas si on multiplie ou on divise, le dividende et le diviseur par un même nombre.
Exemple :
|
|
Dans la division 
, on cherche à
calculer combien de fois il y a le nombre diviseur (27) dans le nombre
dividende (1029).
On choisit le nombre supérieur à 27
On fait la soustraction
On abaisse le chiffre suivant
On fait la soustraction
Lorsqu’on divise deux nombres décimaux à virgule, on utilise la propriété sur « les quotients qui ne changent pas », de façon à transformer le diviseur en nombre entier.
Attention à la virgule
