- Axe de symétrie d’un segment
- Construction à l’équerre
- étape 1
- étape 2
- étape 3
- étape 4
- étape 5
- étape 6
- étape 7
- Construction au compas
- étape 1
- étape 2
- étape 3
- étape 4
- étape 5
- étape 6
- Axe de symétrie d’un angle
- Construction au rapporteur
- étape 1
- étape 2
- étape 3
- étape 4
- étape 5
- étape 6
- Axes de symétrie du cercle
- Construction à la règle
- étape 1
- étape 2
- étape 3
- étape 4
- Axes de symétrie de polygones particuliers
- Triangle isocèle
- Triangle équilatéral
- Cerf-volant
- Rectangle
- Losange
- Carré
- étape 1
- étape 2
- étape 3
- étape 4
- étape 5
- étape 6
La médiatrice d'un segment est l'axe de symétrie de ce segment.
On utilise une règle graduée et une équerre.
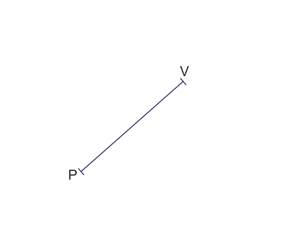
Soit un segment [PV] de longueur 3,6 cm.
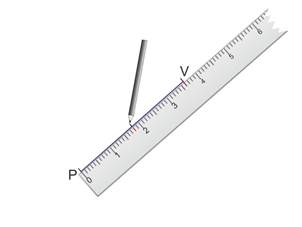
Placer le milieu M du segment à 1,8 cm de P.
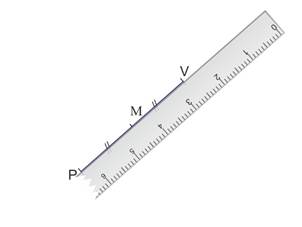
Après avoir codé les égalités de longueur, replacer la règle le long du segment.
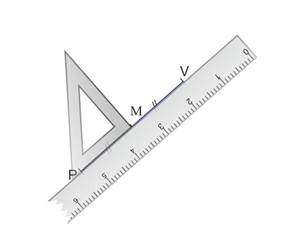
Placer l’équerre le long de la règle, et la faire glisser jusqu’à M.
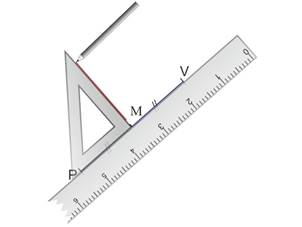
Tracer la droite le long de l’équerre…
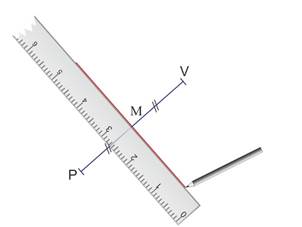
… puis la prolonger avec la règle.
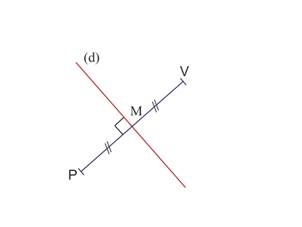
Nommer la droite et coder l’angle droit
(d) est la médiatrice du segment [PV]
On utilise un compas et une règle
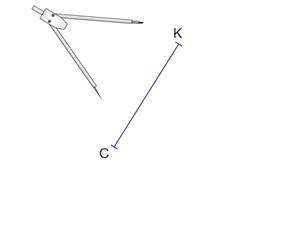
Soit un segment [CK], prendre une ouverture compas supérieure à la moitié de sa longueur.
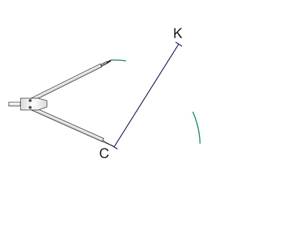
Piquer le compas en C et tracer deux arcs de cercle de part et d’autre du segment.
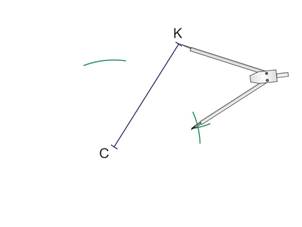
Sans changer l’ouverture du compas, le piquer en K et tracer 2 arcs de cercle coupant ..
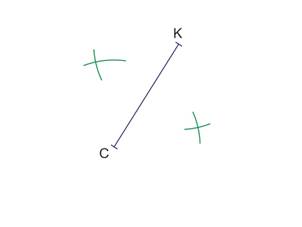
… les arcs précédents.
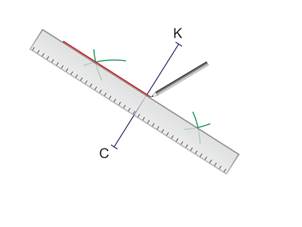
Prendre la règle et tracer la droite passant par les deux intersections.
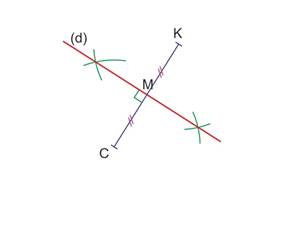
Nommer la droite. C’est la médiatrice de [CK]. Coder ses propriétés.
La bissectrice d'un angle est l'axe de symétrie de cet angle
On utilise un rapporteu r et une règle
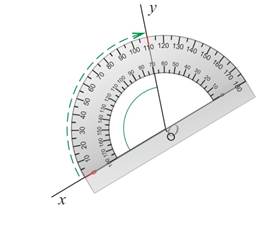
On utilise le rapporteur pour mesurer l’angle. Ici, ![]()
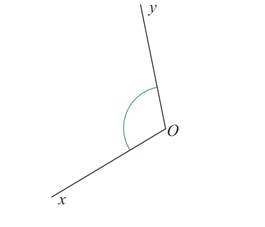
On calcule la moitié de la valeur de l’angle. Ici, ![]()

Avec le rapporteur on repère la graduation 55°
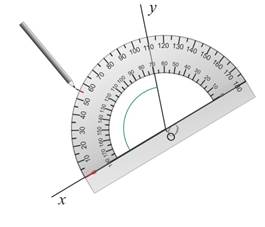
On marque au crayon sa position
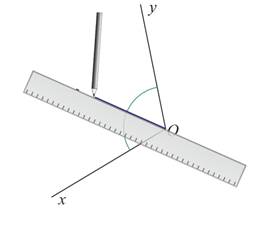
Avec la règle on trace la droite reliant le point au sommet de l’angle.
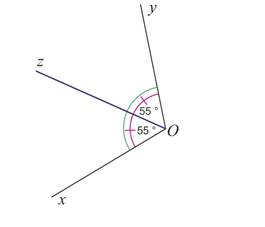
[Oz) est la bissectrice de l’angle ![]()
Un axe de symétrie d’un cercle est confondu avec un de ses diamètres.
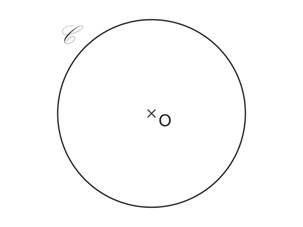
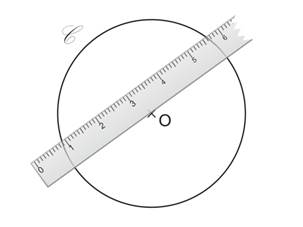
On place la règle au bord du centre O.
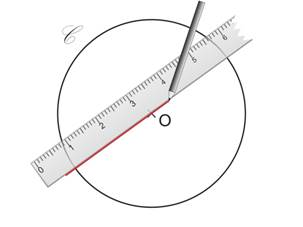
Avec le crayon on trace la droite passant par O.
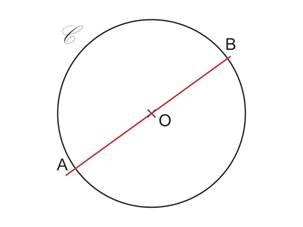
On obtient un diamètre qui est un axe de symétrie du cercle.
Remarque :
Un cercle possède une infinité d’axes de symétrie.
Le triangle isocèle possède un axe de symétrie qui est médiatrice de la base et bissectrice de l’angle du sommet principal.
Construction au compas
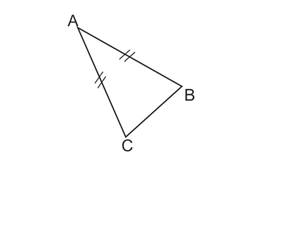
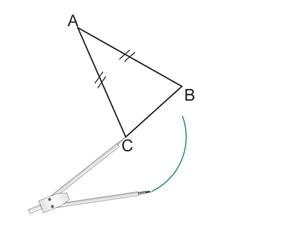
De C comme centre, on trace un arc de cercle suffisamment grand.
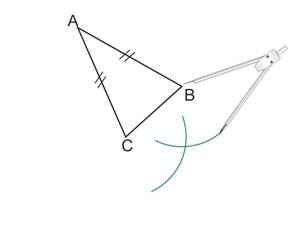
Sans changer l’ouverture de compas, on pique le compas en B et on trace un arc de cercle qui coupe le premier.
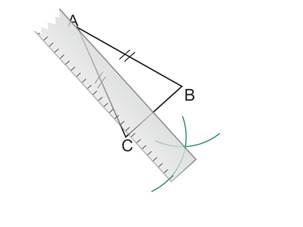
On place la règle entre le sommet principal A et l’intersection des deux arcs.
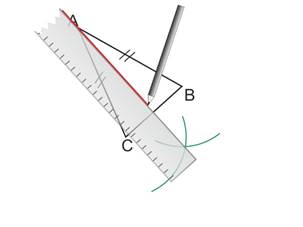
On trace la droite passant par ces deux points.
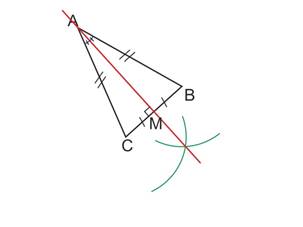
(AM) est l’axe de symétrie de ABC, elle est médiatrice de
[AB] et bissectrice de ![]()
Le triangle équilatéral possède trois axes de symétrie qui sont les médiatrices des côtés et les bissectrices des angles.
Construction
Il suffit de refaire 3 fois la même construction que pour le triangle isocèle
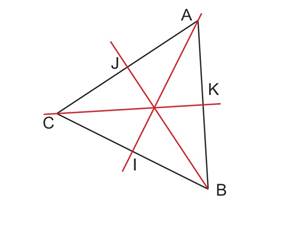
Les droites (AI), (BJ) et (CK) sont les 3 axes de symétrie du triangle équilatéral ABC .
Elles sont respectivement médiatrices des côtés [BC], [CA] et [AB], et bissectrices des
angles ![]()
![]() et
et ![]() .
.
Le cerf-volant possède un axe de symétrie qui est une diagonale.
Construction
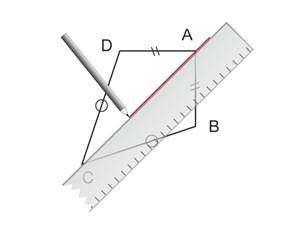
A l’aide d’une règle, on trace la droite passant par les sommets A et C
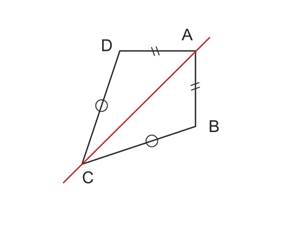
L’axe de symétrie du cerf-volant est la diagonale (AC)
Le rectangle possède deux axes de symétrie qui sont les médiatrices communes des côtés opposés.
Construction

Il suffit de construire par exemple la médiatrice de [AB] (c’est aussi celle de [CD]) et la médiatrice de [AD] (c’est aussi celle de [BC]).
On peut aussi relier les milieux des côtés opposés (si on les connait).
Le losange possède deux axes de symétrie qui sont les diagonales.
Construction
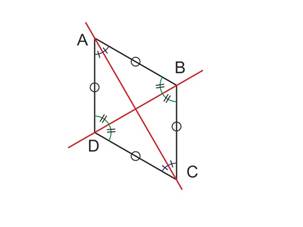
Il suffit de relier les sommets opposés.
Les axes de symétrie sont les bissectrices des angles
Le carré possède quatre axes de symétrie qui sont les diagonales et les médiatrices des côtés.
Construction
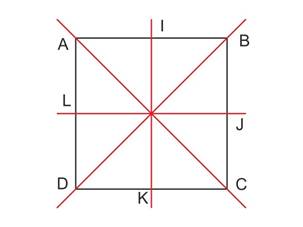
Il suffit de faire comme avec le rectangle et comme avec le losange.