- Définitions
- Symétrie axiale
- Symétrie centrale
Une symétrie axiale est une symétrie par rapport à une droite.
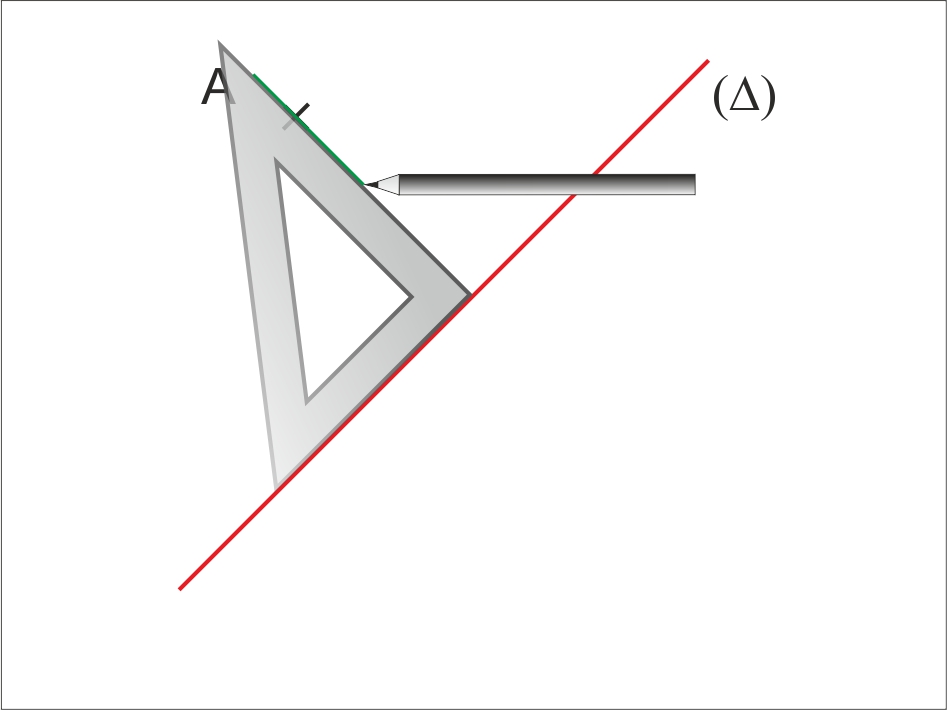
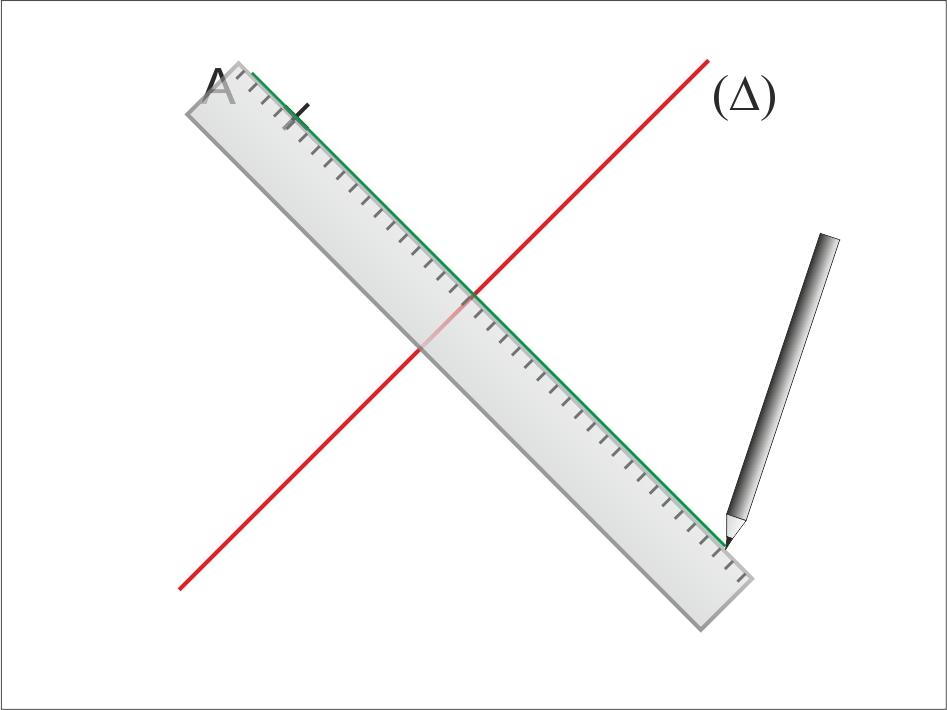
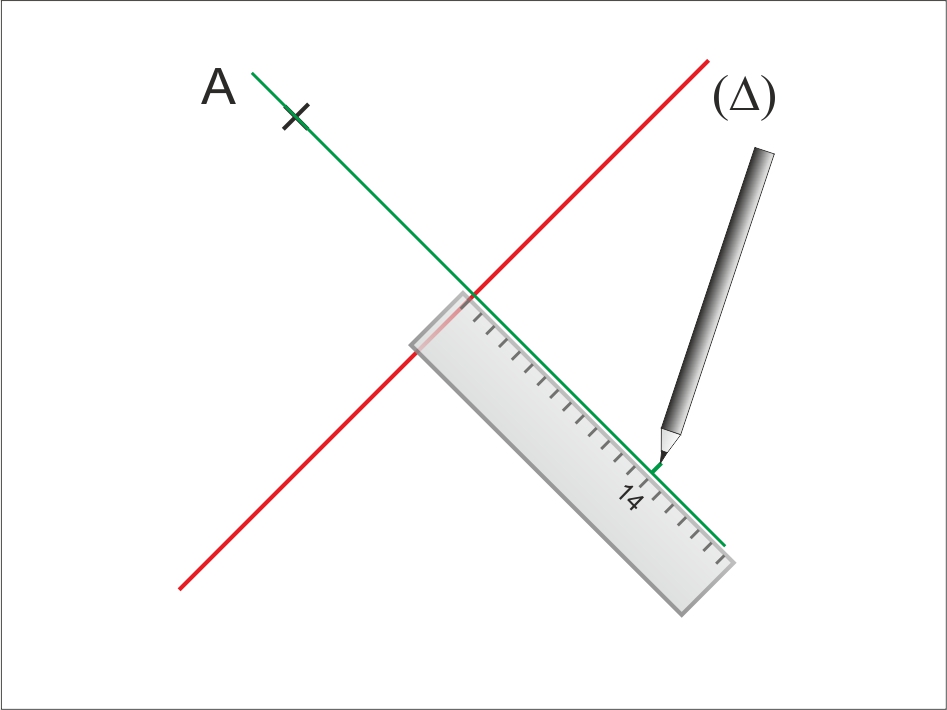
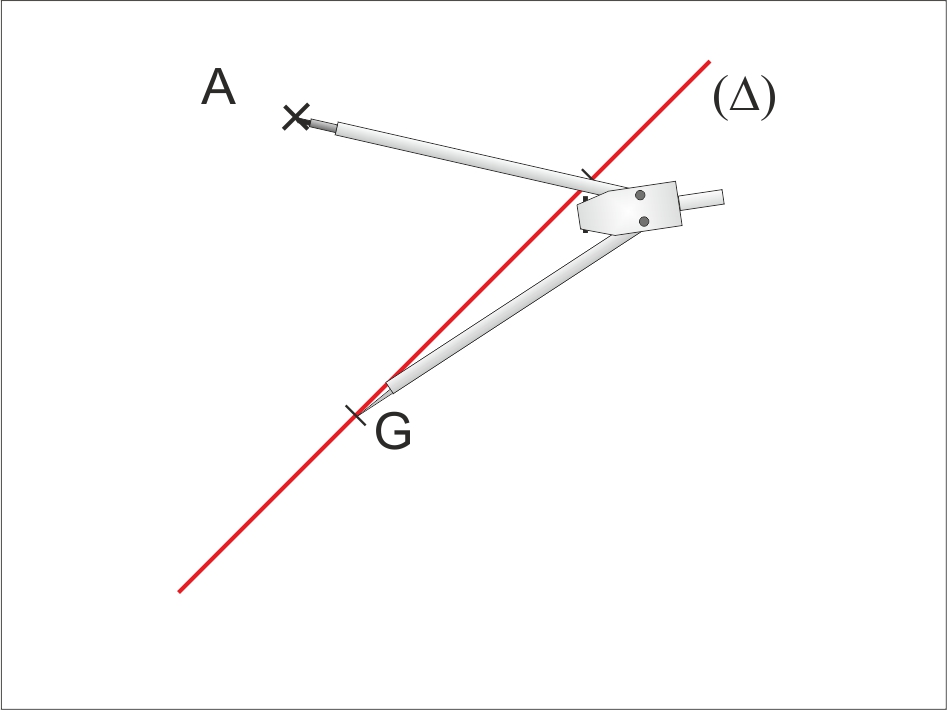
Le symétrique d’un point A par rapport à une droite (D) est un point A’ tel que (D) est la médiatrice de [AA’].
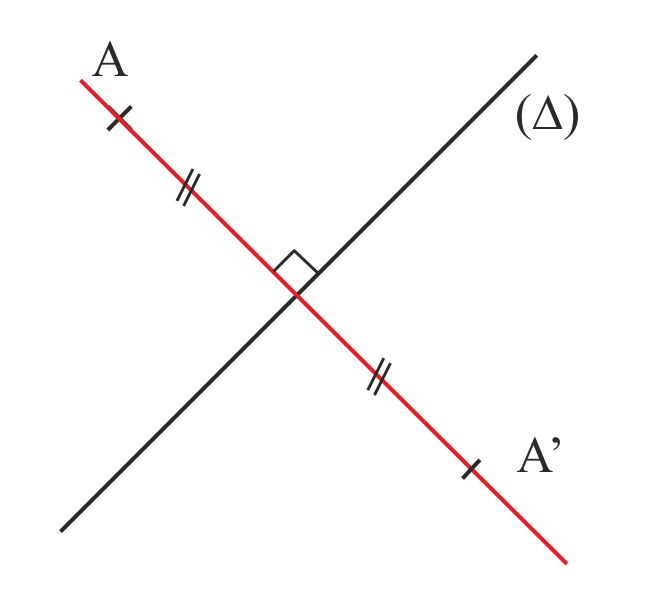
On dit que :
A’ est le symétrique ou l’image de A par rapport à (D).
A et A’ sont symétriques par rapport à (D).
Une symétrie centrale est une symétrie par rapport à un point.
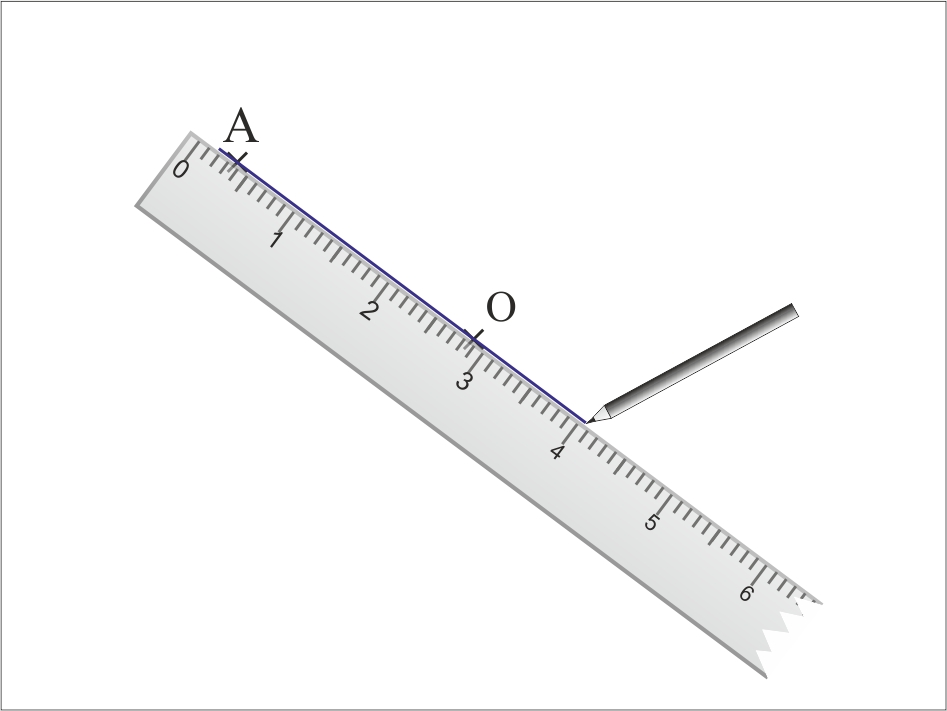
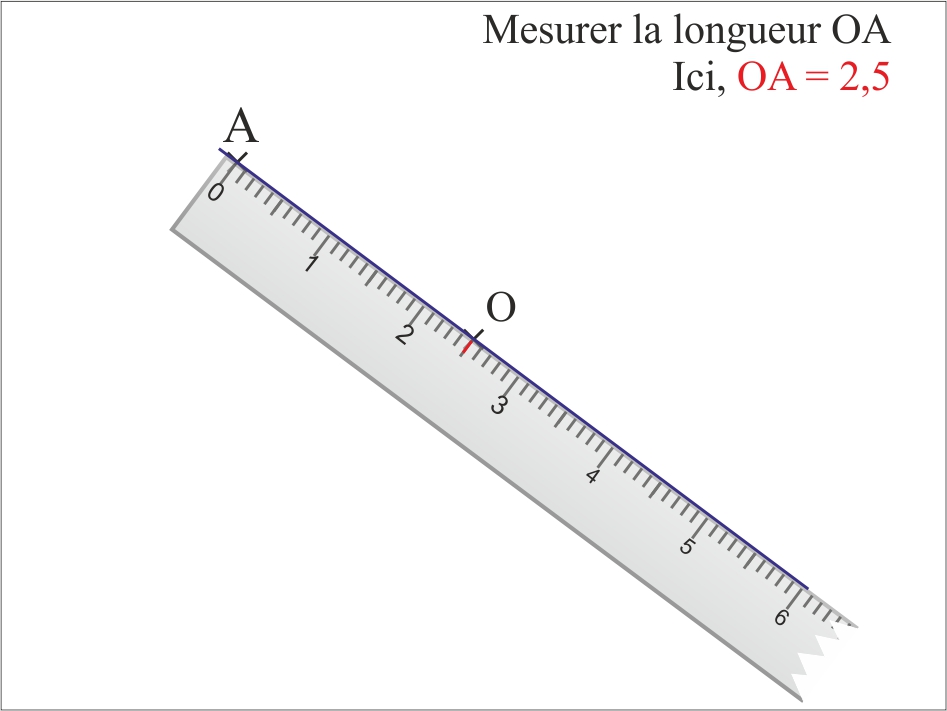
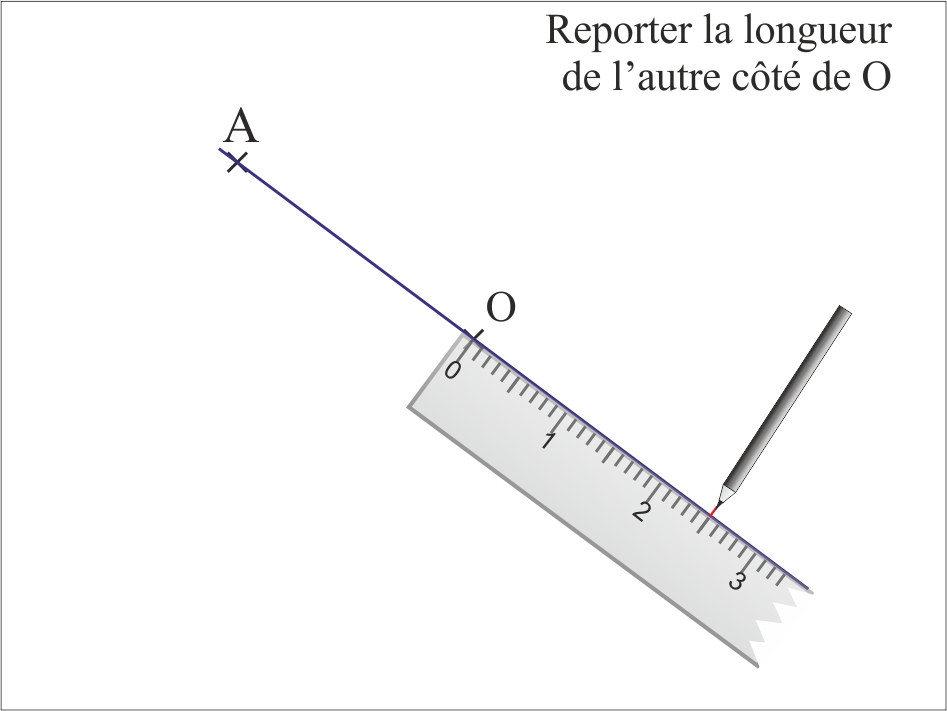
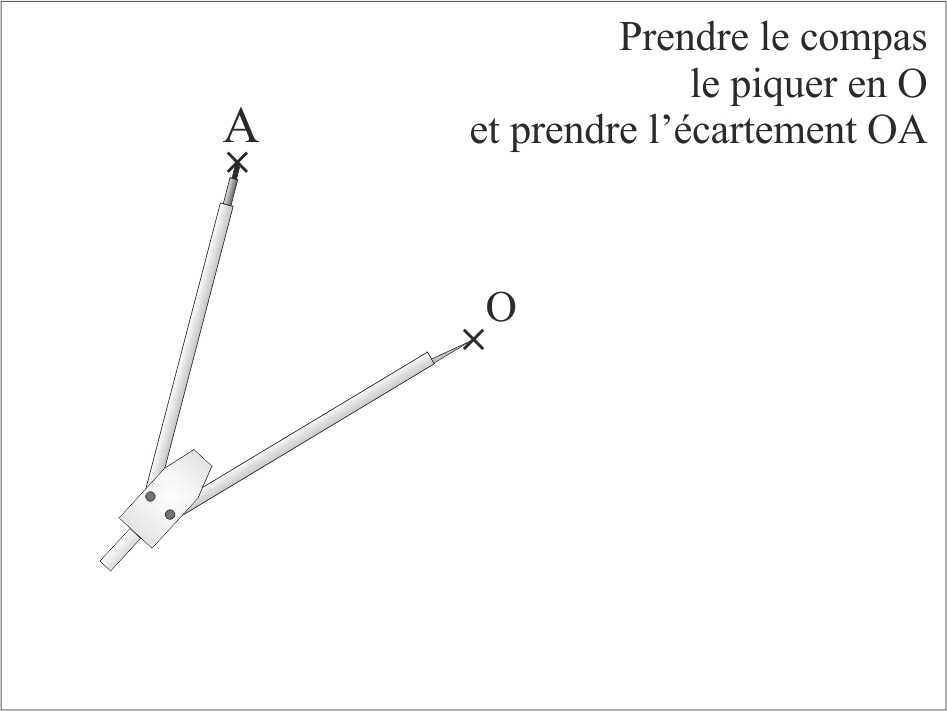
Le symétrique d’un point A par rapport à un point O est un point A’ tel que O est le milieu de [AA’].
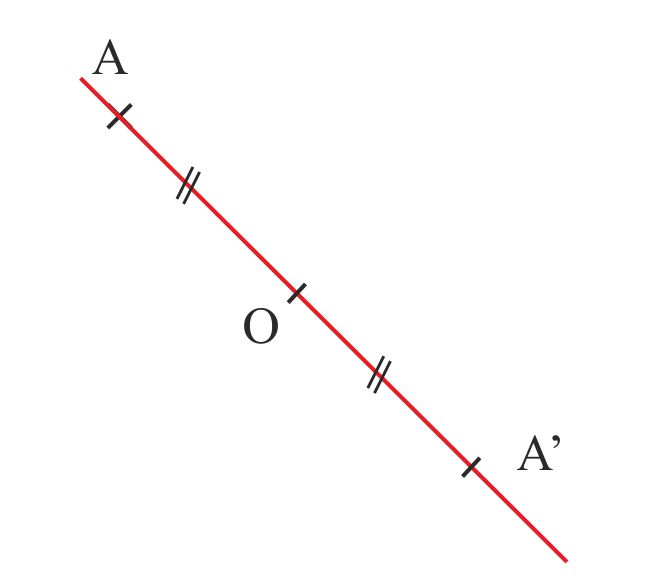
On dit que :
A’ est le symétrique ou l’image de A par rapport à O.
A et A’ sont symétriques par rapport à O.
- Constructions
- Propriétés
- Image d'un segment
- Image d'une droite
- Image d'un angle
- Image d'un cercle
- Par symétrie axiale
- Par symétrie centrale
Par une symétrie axiale, le symétrique d’un segment est un segment de même longueur.
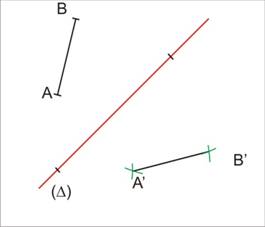
Si [A’B’] est le symétrique de [AB] par rapport à (D)
alors A’B’ = AB
Par une symétrie centrale, le symétrique d’un segment est un segment de même longueur.
Si [A’B’] est le symétrique de [AB] par rapport à O
alors A’B’ = AB
- Par symétrie axiale
- Par symétrie centrale
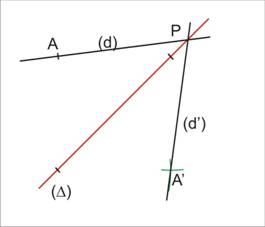
Si (d’) est la symétrique de (d) par rapport à (D)
alors (d) et (d’) se coupent sur (D)
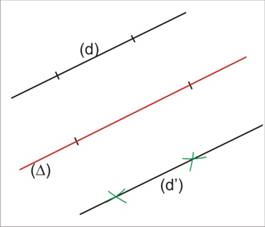
Si (d’) est la symétrique de (d) par rapport à (D) et si (d) // (D)
alors (d’) // (d)
Par une symétrie centrale, deux droites symétriques sont parallèles.
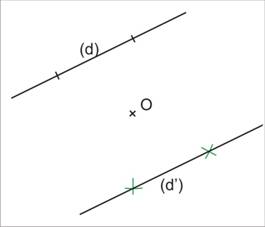
Si (d’) est la symétrique de (d) par rapport à O
alors (d’) // (d)
- Par symétrie axiale
- Par symétrie centrale
Par une symétrie axiale, le symétrique d’un angle est un angle de même mesure
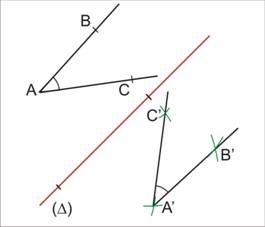
Si 
est le symétrique de 
par rapport à (D)
alors 
Par une symétrie centrale, le symétrique d’un angle est un angle de même mesure
Si est le symétrique de par rapport à O
alors
- Par symétrie axiale
- Par symétrie centrale
Par une symétrie axiale, le symétrique d’un cercle est un cercle de même rayon, leurs centres sont symétriques par rapport à l’axe.
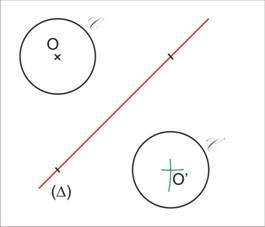
Si C’ (O’, r’) est le symétrique de C (O, r) par rapport à (D) alors r’ = r et O’ est le symétrique de O par rapport à (D)
Par une symétrie centrale, le symétrique d’un cercle est un cercle de même rayon, leurs centres sont symétriques par rapport au centre de symétrie.
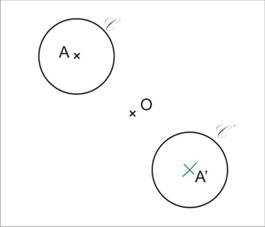
Si C’ (A’, r’) est le symétrique de C (A, r) par rapport à O alors r’ = r et A’ est le symétrique de A par rapport à O
- Eléments de symétrie
- Définitions
- Exemples
Un élément de symétrie d’une figure est un axe de symétrie ou un centre de symétrie de cette figure.
- Une figure géométrique possède un axe de symétrie lorsque chaque point de la figure a son symétrique sur la figure elle-même par rapport à cet axe.
- Une figure géométrique possède un centre de symétrie lorsque chaque point de la figure a son symétrique sur la figure elle-même par ce centre.
|
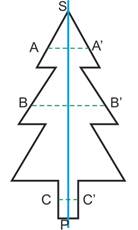
Ce sapin a un élément de symétrie qui est un axe de symétrie |
|
|
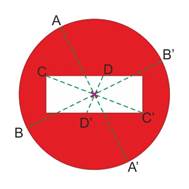
Ce panneau de sens interdit a un élément de symétrie qui est un centre de symétrie |
|
|
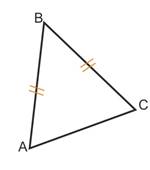
Un triangle isocèle a un élément de symétrie qui est un axe de symétrie |
|
