- Pyramides
- Définitions
- Pyramides régulières
- Patrons
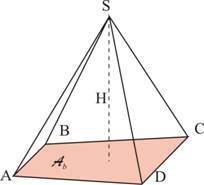
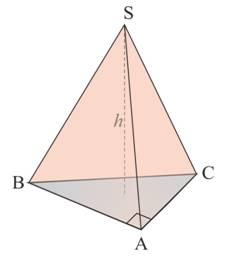
Une pyramide est un solide composée de :
La hauteur H est la longueur du segment issu du sommet et perpendiculaire à la base |
|
Une pyramide régulière est une pyramide dont la base est un polygone régulier et dont les faces latérales sont des triangles isocèles superposables.
Exemples :
|
|
Pyramide régulière à base triangulaire |
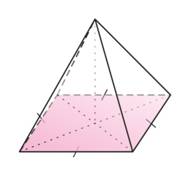
Pyramide régulière à base carrée |
Remarque :
La pyramide régulière à base triangulaire représentée est un cas particulier :
Ses 4 faces sont des triangles équilatéraux superposables. Elle se nomme un tétraèdre
|
|
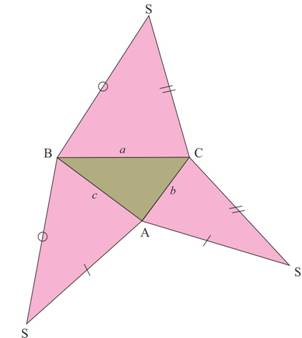
Patron d’un prisme à base triangulaire quelconque |
Le même avec les arêtes latérales égales |
- Cônes de révolution
- Définitions
- Patron
|
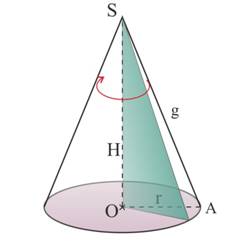
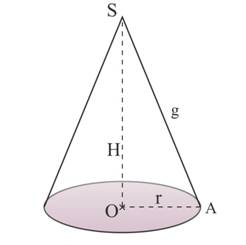
Un cône est engendré par un triangle faisant une révolution autour d’un de ses côtés. Un cône de révolution est composée de :
Remarque : Le segment [AB] représente une génératrice g du cône |
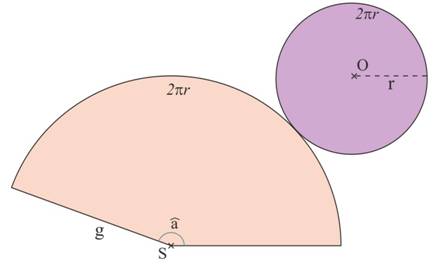
La longueur du secteur du
disque de la surface latérale est égale au périmètre de la base,
doit ![]()
Pour tracer le
patron d’un cône, il faut connaitre la valeur de l’angle ![]() .
.
Sachant qu’elle est proportionnelle à la longueur du secteur du grand disque, on peut établir le tableau suivant :
Disque complet |
Secteur utile |
|
Périmètre |
|
|
Angle |
360 ° |
a |
![]()
![]()
![]()
Exemple :
Soit à faire le patron d’un cône de base de 4 cm de rayon et de génératrice de 10 cm. Quelle sera la mesure de l’angle du secteur du disque latéral ?
![]()
![]()
![]()
- Calculs des volumes
Le volume d’une pyramide ou d’un cône, se calcule de façon identique en utilisant la formule suivante :
![]()
Ab représente l’aire de la base H représente la hauteur
- Exemple d’une pyramide
- Exemple d’un cône
|
Calculer le volume d’une
pyramide de hauteur La base étant un triangle rectangle, son aire est :
Calcul du volume :
|
|
Calculer le volume d’un
cône de hauteur La base d’un cône est un cercle donc son aire est :
Donc le calcul du volume devient :
Soit :
|
- première sous-partie
- deuxième sous-partie
- troisième sous-partie