- Notion de distance
- Distance entre deux points
- Distance entre un point et une droite
- Distance entre deux droites parallèles
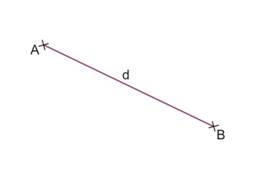
La distance entre deux points est la longueur du segmentqui a pour extrémités ces deux points.
|
La distance entre A et B est la longueur : A B = d Ici, d = 5 cm |
La distance d'un point à une droite est la plus petite distance entre ce point et un point de la droite.
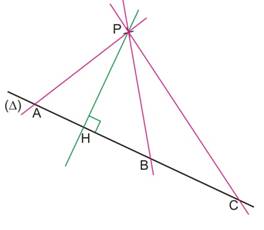
La distance d'un point P à une droite (D) est la longueur du segment qui a pour extrémités le point P et le point d'intersection H de la perpendiculaire à (D) issue de P.
|
La distance entre P et (D) est la longueur : PH = d Ici, d = 2,8 cm |
|
PH < PA PH < PB < PC |
Remarques :
- Si un point P appartient à la droite (D) alors la distance de P à (D) est égale à zéro.
- Si un triangle est rectangle alors l'hypoténuse est son plus grand côté.
La distance entre deux droites parallèles est la longueur du segment qui a pour extrémités les points d'intersection d'une perpendiculaire aux deux droites.
|
La distance entre (D) et (D¢) est la longueur : MN = d Ici, d = 3 cm |
- La tangente à un cercle
- Définition
- Propriété :
- Réciproque :
- Construction d'une tangente au compas :
La tangente à un cercle est une droite qui coupe le cercle en un seul point.
|
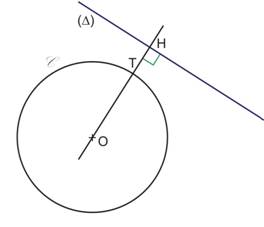
La droite (D) et le cercle C ont le seul point T commun donc la droite (D) est tangente au cercle C . |
Si une droite est tangente à un cercle en un point, alors elle est perpendiculaire au rayon du cercle en ce point.
|
Si (D) est tangente au cercle C en T alors, (D) est perpendiculaire au rayon (OT) Remarque : La distance du centre d'un cercle à une de ses tangentes est égale à un rayon du cercle. |
Positions relatives d'une droite et d'un cercle :
|
|
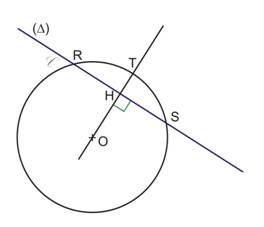
Si OH < OT, alors la droite (D) est sécante au cercle C |
Si OH > OT, alors la droite (D) est extérieure au cercle C |
Si une droite est perpendiculaire à un rayon d'un cercle en son extrémité, alors, elle est tangente au cercle.
|
Si (D) est perpendiculaire au rayon (OT) en T alors, (D) est tangente au cercle C en T |
Cela revient à construire la médiatrice du segment d'extrémité le centre du cercle et de milieu le point de tangence.
Voir l'animation de la méthode de construction au compas
- Bissectrices d'un angle et cercle inscrit
- Bissectrice d'un angle
- Cercle inscrit dans un triangle
- Définition et construction
- Propriété et construction
La bissectrice d'un angle est une demi-droite qui partage cet angle en deux angles de même mesure.
|
Pour construire cette bissectrice on peut utiliser un rapporteur et une règle
Voir l'animation de la méthode de construction au rapporteur
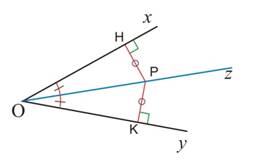
Chaque point d'une bissectrice d'un angle est à égale distance des deux côtés de cet angle.
|
Si P Î (Oz) Alors, PH = PK |
Pour construire cette bissectrice on peut utiliser une règle graduée et une équerre.
Voir l'animation de la méthode de construction à l'équerre
Pour construire cette bissectrice on peut utiliser un compas et une règle.
Voir l'animation de la méthode de construction au compas
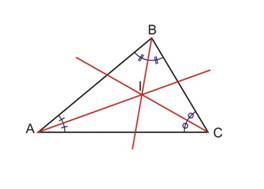
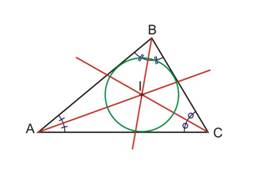
Les trois bissectrices d'un triangle se coupent en un point qui est le centre du cercle inscrit à ce triangle.
|
|
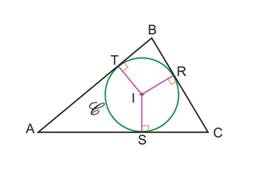
Un cercle est inscrit dans un triangle si ses trois côtés sont tangents à ce cercle.
|
Si (AB), (BC) et (CA) sont tangentes à C, alors, le cercle C est inscrit dans le triangle ABC |