- Le Théorème de Thalès
Le théorème de Thalès sert à calculer une longueur ou à construire des points.
- Calculer une longueur
- Construire des points
 |
 |
- Conditions à satisfaire
- Enoncé de Thalès
- Exemple de calcul de longueur
- Agrandissement ou réduction
- Avoir deux droites sécantes coupées par deux droites parallèles.
- Connaître les longueurs de trois segments pour calculer la longueur d’un quatrième.
Si deux droites sécantes sont coupées par deux droites parallèles, alors elles forment deux triangles aux côtés associés proportionnels.
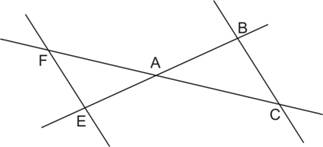
Soit (EB) et (FC) deux droites sécantes en A telles que AB = 9 cm ; AE = 3 cm ; EF = 4,2 cm et (EF) et (BC) sont parallèles.
Calculer BC..
On sait que si (EB) et (FC) sont deux droites sécantes en A que AB=9 cm; AE=3 cm; EF=4,2 cm et que (EF) est parallèle à (BC) alors d’après le théorème de Thalès, ABC et AEF ont leurs côtés associés proportionnels
| Longueurs de ABC |  |
 |
 |
| Longueurs de AEF |  |
 |
 |
D'où :
Si deux figures de même forme (semblables), ont leurs côtés associés proportionnels, on dit que l’une est un agrandissement ou une réduction de l’autre.
Le coefficient de proportionnalité étant « k » :
- Si
,
il s’agit d’une réduction. - Si
,
il s’agit d’un agrandissement.
Dans un agrandissement ou une réduction de coefficient « k », les longueurs de la figure agrandie ou réduite sont calculées en multipliant celles de la figure initiale par « k ».
Remarque :
Dans ce cas, les deux figures ont les mêmes angles, la perpendicularité et le parallélisme sont conservés.
- Construction d'un point particulier sur un segment
- Construction de deux points sur une droite
Tracer un segment [AB].
Construire le point M du segment [AB] tel que :
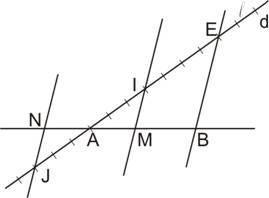
Solution : On trace la droite d passant par A. Sur cette droite à partir de A, on dessine des segments consécutifs de même longueur, l. Soit I et E les points de la droite d tels que : AI = 5 × l et AE = 7 × l On trace la droite (BE) et la parallèle à (BE) passant par I. Cette droite coupe la droite (AB) en M. D'après le théorème de Thalès :
|
|
- Premier cas
- Deuxième cas
Tracer un segment [AB].
Construire les points M et N de la droite (AB) tel que :
Solution : Traçons le segment [AB]. Traçons la droite d passant par A. Sur cette droite à partir de A, traçons des segments consécutifs de même longueur, l. Soit I et J les points de la droite d tels que : AI = AJ = 3 × l Soit E le point de cette droite tel que : AE = 7 × l Traçons la droite (BE) et les parallèles à (BE) passant par I et J. Ces droites coupent la droite (AB) en M et N. D'après le théorème de Thalès :
Donc :
|
|
Tracer un segment [AB].
Construire les points M et N de la droite (AB) tel que :
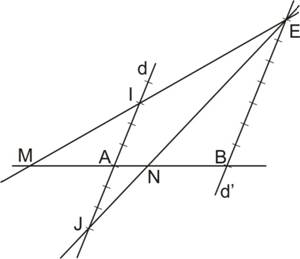
Solution : Traçons le segment [AB]. Traçons deux droites d et d' parallèles passant respectivement par A et B. Sur ces droites à partir de A et B, traçons des segments consécutifs de même longueur, l. Soit I et J les points de la droite d tels que : AI = AJ = 3 × l Soit E le point de la droite d' tel que : BE = 7 × l. Traçons les droites (EI) et (EJ). Ces droites coupent la droite (AB) en M et N. D'après le théorème de Thalès :
Donc : |
|
- Réciproque du théorème de Thalès
La réciproque du théorème de Thalès sert à démontrer que deux droites sont parallèles.
- Conditions à satisfaire
- Configurations possibles
- Énoncé
- Exercice d'application
- Avoir deux droites sécantes coupées par deux autres droites semblant être parallèles.
- Connaître les longueurs de quatre segments, deux à deux correspondants, dont les quotients sont égaux.
- Avoir des points alignés dans le même ordre sur chaque droite
|
|
Si deux triangles sont formés par deux droites sécantes et deux autres droites et que leurs côtés associés sont proportionnels, alors ces deux autres droites sont parallèles.
Dans les triangles ABC et AEF d'une configuration de Thalès,
si les points A, E et B d'une part et A, F et C d'autre part sont alignés dans cet ordre,
et si 
(ou 
ou 
),
alors les droites (BC) et (EF) sont parallèles.
On démontre que deux droites sont parallèles
Soit (EB) et (FC) deux droites sécantes en A telles que AB = 9 cm ; AE = 3 cm ; EF = 4,2 cm et BC = 12,6 cm.
Les droites (EF) et (BC) sont-elles parallèles ? Pourquoi ?
On sait que (EB) et (FC) sont deux droites sécantes en A que AB = 9 cm; AE = 3 cm; EF = 4,2 cm et que BC = 12,6 cm
| Longueurs de ABC | |
|
 |
| Longueurs de AEF | |
|
|
Remarque :
Pour comparer des quotients, on peut envisager trois types de stratégie :
- Calculer les quotients en comparant ensuite les nombres décimaux de façon rigoureuse.
- Réduire les quotients aux mêmes dénominateurs ou aux mêmes numérateurs pour pouvoir les comparer.
- Considérer qu'une égalité de quotient correspond à une égalité de produits, et comparer les produits associés.
On calcule les quotients :
Ou alors on réduit au même dénominateur :
Ou alors on calcule les produits associés :
Par conséquent :
Donc, puisque et que les points E, A et B d'une part, et F, A et C d'autre
part, sont alignés dans le même ordre, alors, d'après la
réciproque du théorème de Thalès, les
droites (EF) et (BC) sont parallèles.
- Contraposée du théorème de Thalès
La contraposée du théorème de Thalès sert à démontrer que deux droites ne sont pas parallèles.
Enoncé :
Si deux triangles sont formés par deux droites sécantes et deux autres droites et que leurs côtés associés ne sont pas proportionnels, alors ces deux autres droites ne sont pas parallèles.
Exemple :
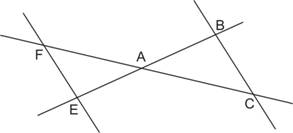
Soit (EB) et (FC) deux droites sécantes en A telles que AB = 5,6 cm ; AE = 2 cm ; EF = 4,2 cm et BC = 11,7 cm.
Les droites (EF) et (BC) sont-elles parallèles ? Pourquoi ?
On sait que (EB) et (FC) sont deux droites sécantes en A que AB = 5,6 cm ; AE = 2 cm ; EF = 4,2 cm et BC = 11,7 cm.
| ABC | AB | AC | BC |
| AEF | AE | AF | EF |
On calcule :
Ou alors
Ou alors
Par
conséquent :
Donc puisque, alors les droites (EF) et (BC) ne
sont pas parallèles