- Angle inscrit et angle au centre
- Définitions
- Propriétés
- Angle inscrit
- Angle au centre
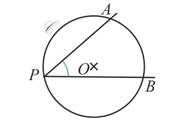
Un angle inscrit est un angle qui à pour sommet un point d’un cercle et dont les deux côtés coupent le cercle en deux points
|
|
On dit que l’angle inscrit ![]() intercepte l’arc de cercle
intercepte l’arc de cercle ![]() et
qu’il est inscrit dans le cercle C.
et
qu’il est inscrit dans le cercle C.
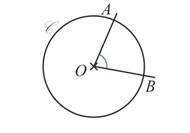
Un angle au centre est un angle qui a pour sommet le centre d’un cercle et ses deux côtés coupent le cercle en deux points.
|
|
On dit que l’angle au centre ![]() intercepte l’arc de cercle
intercepte l’arc de cercle ![]() .
.
- Propriété 1
- Propriété 2
Si un angle inscrit intercepte le même arc de cercle qu’un angle au centre alors la mesure de l’angle au centre est le double de celui de l’angle inscrit.
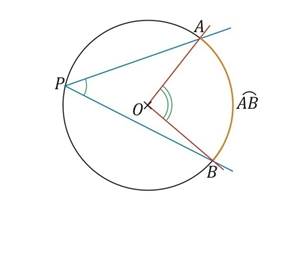
![]()
Si deux angles inscrits interceptent le même arc de cercle alors ils ont même mesure.
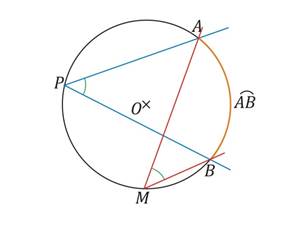
![]()
- Les polygones réguliers
- Définition
- Propriétés
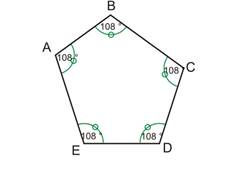
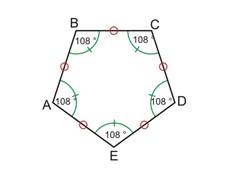
Un polygone régulier est un polygone dont tous les côtés ont la même longueur et dont tous les angles ont la même mesure.
- Exemple général : le pentagone
- Exemples particuliers :
C'est un polygone à 5 côtés.
Pentagone quelconque (convexe) |
Pentagone quelconque (concave) |
Pentagone à côtés égaux |
Pentagone à angles égaux |
Pentagone croisé |
Pentagone régulier (côtés et angles égaux) |
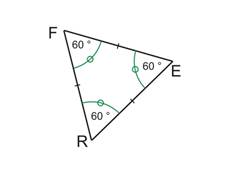
- Polygone régulier à trois côtés :
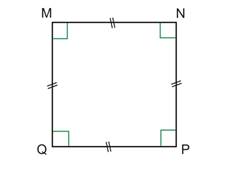
- Polygone régulier à quatre côtés :
- Polygone régulier à six côtés :
|
Un triangle équilatéral a ses trois côtés de même mesure et ses trois angles égaux à 60 °. |
|
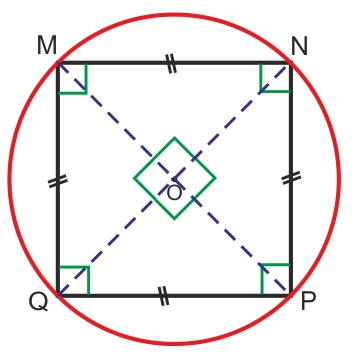
Un carré a ses quatre côtés de même longueur et ses quatre angles droits (90 °). |
|
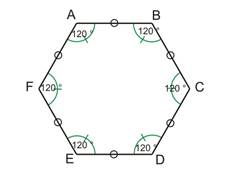
Un hexagone régulier a ses six côtés de même longueur et ses six angles égaux à 120 ° |
- Propriété 1
- Propriété 2
- Propriété 3
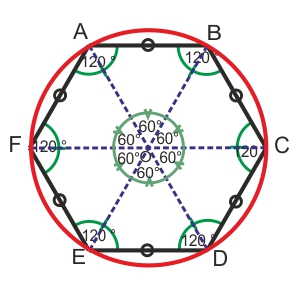
Tous les sommets d’un polygone régulier appartiennent à un même cercle, on dit alors qu’il est inscrit dans un cercle dont le centre est appelé le centre du polygone régulier.
Exemple : l'hexagone régulier
|
L'hexagone ABCDEF a tous ces sommets sur le cercle de centre O, il est inscrit dans ce cercle et O est son centre |
Si un polygone est inscrit dans un cercle et qu’il a tous ses côtés de même longueur alors ce polygone est régulier.
Exemples
|
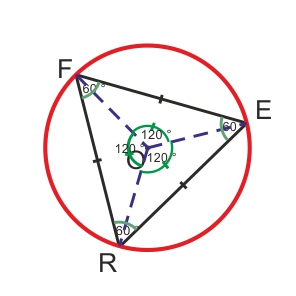
Un triangle équilatéral est inscrit dans un cercle et a trois côtés de même longueur, donc le triangle équilatéral est un polygone régulier. |
|
Un carré est inscrit dans un cercle et a quatre côtés de même longueur, donc le carré est un polygone régulier. |
Si A et B sont deux sommets consécutifs d’un polygone régulier à « n » côtés de centre O alors
l’angle ![]() est appelé angle
au centre du polygone et sa mesure est égale
à
est appelé angle
au centre du polygone et sa mesure est égale
à ![]() .
.
« n » est un nombre entier positif.
Polygone |
Triangle |
Carré |
Pentagone |
Hexagone |
|
120 |
90 |
72 |
60 |